Massive quantum entanglement

Computer science • Physics • Quantum physics • Science • Technology
By Francisco R. Villatoro 2 comments Print
Figure 1: Example of two-dimensional subspace for measurement of the spatial shape of a photon; intensities and phases for two modes in the z basis, and their superposition leading to a mode in the x basis. | Credit: Krenn et al (2013)
Figure 1: Example of two-dimensional subspace for measurement of the spatial shape of a photon; intensities and phases for two modes in the z basis, and their superposition leading to a mode in the x basis. | Credit: Krenn et al (2013)

Entanglement is a fundamental tool in quantum computing and several quantum information protocols, such as quantum teleportation, quantum cryptography and quantum key distribution. The basic unit of entanglement is the entangled bit (ebit), represented by a maximally entangled state of two qubits (quantum bits). Entanglement can also be implemented in a higher dimensional Hilbert space using qudits, the multilevel version of qubits using d levels instead of 2. The great advantage of using qudits is that the resulting high-dimensional entangled system is more robust to noise and decoherence than a system with the same dimension using qubits. However, the determination of the exact dimension of entanglement (the number of ebits) is very difficult using standard quantum state tomography, due to the large dimensionality of the Hilbert space.

The Austrian quantum physicist Anton Zeilinger (University of Vienna), eternal candidate to the Nobel Prize in Physics, and several colleagues 1 have developed a new criterion that reveals massive quantum entanglement in high-dimensional qudit systems. Although the new proposal is based on a mathematical conjecture, there is strong numerical evidence and theoretical arguments supporting its correctness. The nonlinear criterion has been used to verify the non-maximal entanglement of at least 103 ebits in a (186*186)-dimensional Hilbert space based on two photons entangled in spatial shape acting as a pair of qudits. This is the largest entangled multipartite system experimentally measured so far.

Figure 2: Visualization of the measurement concept. Two photons are separated into different paths, being each one in a superposition of many modes. The dimensionality of entanglement is determined performing 12 measurements, two projective measurements on each of the three components of the orbital angular momentum of each photon. | Credit: Krenn et al (2013)
Figure 2: Visualization of the measurement concept. Two photons are separated into different paths, being each one in a superposition of many modes. The dimensionality of entanglement is determined performing 12 measurements, two projective measurements on each of the three components of the orbital angular momentum of each photon. | Credit: Krenn et al (2013)

Entanglement describes the quantum correlations lying at the heart of the parallelism in quantum computers, whose processing power could be exponentially greater than that of conventional computers 2. Being a genuine quantum-mechanical feature which does not exist in the classical world, it accounts for non-local correlations between the parts of a multipartite system in such a way that they cannot be described classically. A qubit is a quantum two-level system described in terms of a Hilbert space with dimension two. A record of n qubits is entangled if their common state is not a product of individual states for each one of the qubits, but instead the superposition of each of the 2n states of the record. The key feature of quantum parallelism is that a physical operation applied to this quantum record is equivalent to its simultaneous application to the whole set of its exponential number of states. The result is a large speedup in certain algorithms (such Shor’s algorithm for integer factoring or Grover’s algorithm for searching an unordered list).

High-dimensional entanglement can also be obtained using a pair of qudits, quantum d-level systems described in terms of a Hilbert space with dimension d ; the result is a (d*d) dimensional Hilbert space, but usually the dimension of the entanglement is not maximal 3. The most common entanglement between two photons is in polarization, by using the superposition of two orthogonal polarizations (a two-dimensional Hilbert space); this option has the limitation that the amount of entanglement is restricted to only one ebit. Two photons can also be entangled in other degrees of freedom, such as frequency and spatial shape by using spontaneous parametric down-conversion (SPDC), a process where the interaction of a strong pump beam with a nonlinear crystal mediates the emission of two lower-frequency photons (signal and idler) [4]. The advantage of frequency and spatial entanglement is that the corresponding Hilbert space has infinite dimensions,offering thus the possibility to implement qudits instead of qubits.

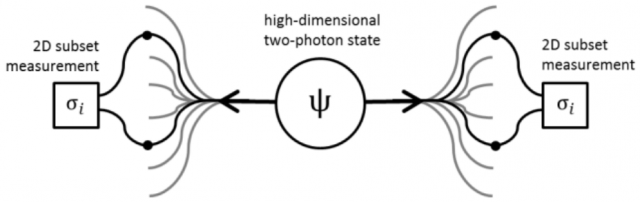
The high-dimensional entanglement of qudits instead of qubits is a double-edged sword, since the huge dimensionality of the Hilbert space is an insurmountable obstacle for the rigorous experimental determination of the entanglement dimension of the system. Quantum state tomography, i.e., a complete reconstruction of the state, is not necessary to determine the entanglement dimension in a non-maximally entangled system, instead the so-called Schmidt decomposition of the entangled state can be done reducing the number of measurements required to its dimension. However, for a pair of 186-level qudits, a prohibitive amount of about 109 measurements of the full Hilbert space is required. Otherwise, a theoretical analysis can be used to obtain an initial estimate of the dimension, but the required approximations avoid an exact analytical calculation. In fact, the entanglement dimension of a pair of photons entangled in spatial shape generated by SPDC depends in a complicated way on the geometry used (collinear vs noncollinear), the length of the nonlinear crystal, and the size of the pump beam. Hence, the practical determination of the dimension of the entanglement needs an experimentally feasible protocol for dimension witnesses 4.

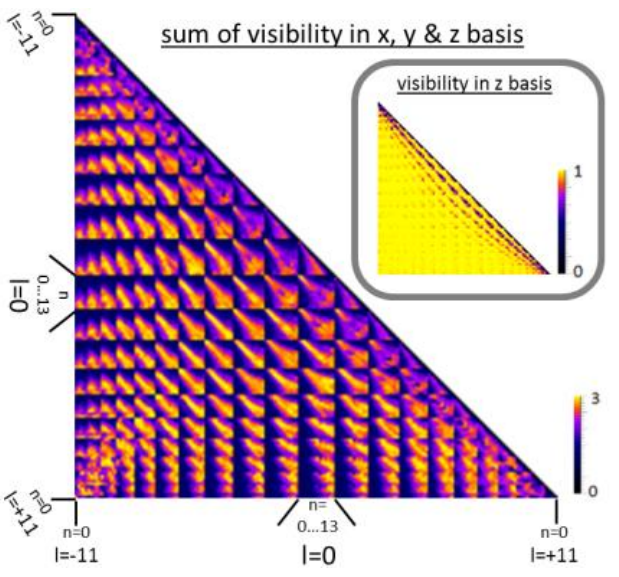
Figure 3: Sum of coincidence visibilities in x, y, and z basis of 17.025 two-dimensional subspaces for the measurement of the three orbital angular momentum components of both photons. For a detailed technical explanation see the caption | Credit: Krenn et al (2013)
Figure 3: Sum of coincidence visibilities in x, y, and z basis of 17.025 two-dimensional subspaces for the measurement of the three orbital angular momentum components of both photons. For a detailed technical explanation see the caption | Credit: Krenn et al (2013)

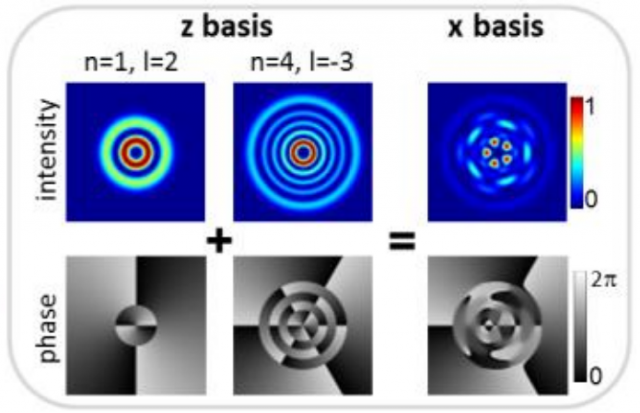
Zeilinger and his colleagues [1] have developed a novel nonlinear entanglement dimension criterion capable of revealing high dimensional entanglement through sub-space correlations. A conjectured bound for these correlations, currently mathematically unproved, but for which the authors have strong numerical evidences and theoretical arguments, reduces the number of measurement settings to only 51.615 (with 206.406 projective measurements) for two qudits in a (186*186)-dimensional Hilbert space; this constitutes about 0,005% of those required for a Schmidt decomposition. The new criterion has been experimentally demonstrated using two photons entangled in orbital momentum and spatial shape generated using SPDC. After its application the authors claim that the analyzed state was entangled in at least 103 dimensions (possibly more, since the conjectured bound is sufficient but not necessary), i.e., 103 ebits.

Figure 4: The correlations (normalized coincidence rate) in the z-basis between the 186 modes (n,l) weighted appropriately for the new criterion. A technical explanation in the caption of Figure 3 of Ref. [1]. | Credit: Krenn et al (2013)
Figure 4: The correlations (normalized coincidence rate) in the z-basis between the 186 modes (n,l) weighted appropriately for the new criterion. A technical explanation in the caption of Figure 3 of Ref. [1]. | Credit: Krenn et al (2013)
The technical details behind the new nonlinear entanglement witness are outside the scope of this post. The new criterion is based on the measurement of the (normalized) coincidences between different modes using three mutually unbiased bases for each component of the orbital angular momentum components of each photon, each one projected in two-dimensional subspaces using single-qubit Pauli matrices, as illustrated in Figs. 3 and 4. Like in opinion polls, where a small sample, a properly selected subset of the whole population, can result in a good estimation of the global opinion, the new criterion yields a good estimation of the entanglement dimensionality using only a small subset of projective measurements.

The paper by Krenn et al has taken my attention not only because of its last author, the reknown physicist Anton Zeilinger, but also because its second author, Marcus Huber is affiliated to The Institue of Photonic Sciences (IFCO) and the Universitat Autònoma de Barcelona. But the most important thing is that the new criterion for estimating the dimension of quantum entanglement in photonic systems using qudits has a great potential for a wide range of quantum information applications where non-maximally entangled states could be used instead of maximal ones.

References

  1. Mario Krenn, Marcus Huber, Robert Fickler, Radek Lapkiewicz, Sven Ramelow, Anton Zeilinger, “Studies of Quantum Entanglement in 100 Dimensions,” arXiv:1306.0096, unpublished preprint submitted to arXiv on 1 June 2013. ↩
  2. Otfried Gühne, Géza Tóth, “Entanglement detection,” Physics Reports 474(1–6): 1–75, April 2009. DOI: 10.1016/j.physrep.2009.02.004 [arXiv:0811.2803]. ↩
  3. S.P. Walborn, C.H. Monken, S. Pádua, P.H. Souto Ribeiro, “Spatial correlations in parametric down-conversion,” Physics Reports 495(4–5): 87–139, October 2010. DOI: 10.1016/j.physrep.2010.06.003 [arXiv:1010.1236]. ↩
  4. Nicolas Brunner, Miguel Navascués, Tamás Vértesi, “Dimension witnesses and quantum state discrimination,” Phys. Rev. Lett. 110, 150501 (2013). DOI: 10.1103/PhysRevLett.110.150501 [arXiv:1209.5643]. ↩

Written by

2 comments

  • Spooky action at a distance, Einstein had a problem with this Quantum entanglement. Relativity and Quantum seem to be implying two very different fundamental root concepts. Relativity and all its formulas has as its root concept that “time and space is some sort of environment that everything including the observer exists IN”, Quantum at every new discovery, including entanglement and superposition, is implying that neither space nor time are what they otherwise seem to be at all, (a persistent illusion as Einstein said) but are something, NOT THAT WE EXIST IN, BUT THAT EXISTS IN US, IN OUR CONSCIOUSNESS. (different root concept) In other words space and time cannot exist without awareness, consciousness or observation. What a quandary for objective independent experiment!!!

    Reply

Leave a Reply

Your email address will not be published.Required fields are marked *