Entangled through a wormhole

A lot of ink has been wasted in the last decades discussing whether string theory is a good description of nature or merely a mathematica construct with no connection at all with reality. However, the answer to this question actually lays at least in the middle of both options and for sure not any close to the second one of them, mainly because the development during the last 20 years of what is called AdS/CFT correspondence or Maldacena’s conjecture has made every single paper published in this time worth (and the Maldacena’s paper¹ introducing it has become the most cited paper in the history of physics).

This conjecture states that any physical quantity of a quantum field theory in 4 dimensions containing gauge fields (as the simplest example of a gauge field, think of electromagnetism) is dual, can be matched one to one, to some physical quantities of a pure gravitational theory in 5 dimensions. Thus, maybe a 5 dimensional world does not exist, but we still can formulate gravity in such imagined world and use it as a mere mathematical tool to easily compute things that in the quantum field theory can be difficult to calculate.

The applications of this duality are huge, spanning from magnetic properties of solid materials to the estimation of the energy spread in an ion collision like the ones performed in the LHC. However, recently Juan M. Maldacena and Leonard Susskind used it to conjecture² an incredible relation between two exotic elements of modern physics, wormholes and quantum entanglement.

Entanglement is a property of quantum physics in which the states of two different particles become related in such a way that measuring one of the particles forces the result of measuring the second particle to be a concrete one. For example, one can entangle the spin of two particles so that when one measures one of them and finds a direction, the result of measuring the other is going to be the same direction always. Just one caveat exists, that the observer measuring the second particle must know the result of the first measure. If she does not know it, it is like if the entanglement does not exists.

This peculiar property of physics relating the measure of the quantum properties of a system and the information that the experimenter retains have made some physicist think that maybe we are missing some fundamental property of nature that relays under the explanation of this phenomena. During a lot of years this discussion has been merely philosophical but, just before the summer of 2013, Maldacena and Susskind proposed to use the AdS/CFT correspondence to study it by constructing the gravitational dual to an entangled state. In order to do that, they proceeded as follows.

First, they took two different gauge fields (corresponding to two different field theories) independent of each other, being the only interaction between them the fact that they are taken in an entangled state, relating their individual states. Specifically, they took it to be in a kind of entanglement named EPR (Einstein-Podolsky-Rosen). Then, they argued that the gravitational situation describing this, having the same physical symmetries, having the same temperature, etc… is an eternal black hole. And this is a very special kind of black hole.

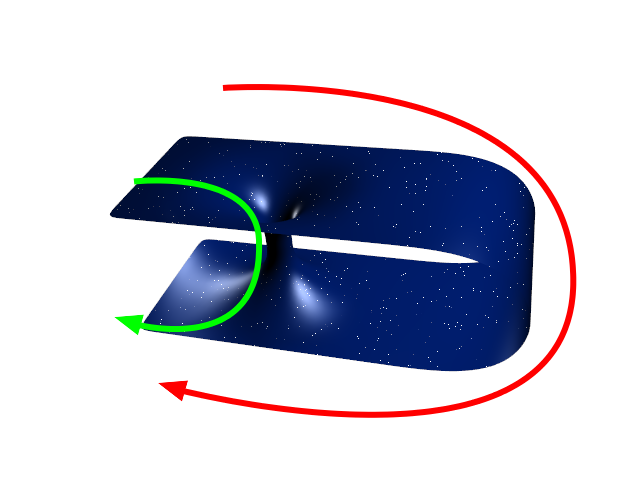
In opposition to a black hole formed by collapsing matter, an eternal black hole has two exteriors. If one study the geometry of spacetime in its presence, we find that there are trajectories (not physical since they require moving faster than light but they still exists) that can go through the interior of the black hole and go out in another different region of space. Therefore, what Maldacena and Susskind argue is that we can identify the two different gauge field as corresponding to the two different exteriors of the black hole.

But, of course, even if the exteriors are different, the two fields are entangled, so some sort of communication must occur between them and the only way to connect them is by using precisely these non-traversable trajectories, which receive the name of wormhole or ER (Einstein-Rosen) bridge.

Therefore, the conjecture of Maldacena and Susskind can be summarized in the simple equation ER=EPR and states that any entanglement is related (via AdS/CFT) to some sort of ER bridge. A quite strong and surprising relation.

Of course, this is just a conjecture (therefore it has not been proven) that relays in another conjecture that, even if it has been extensively checked, it has not been generally proved yet. Therefore, we must be cautious and not take this as a new dogma in physics but just as a very interesting insight in the properties of quantum entanglement and on the nature of reality. Of course, some people³ have started to examine this idea in the recent months by constructed explicit non-general entangled states and computing some of its related physical observables by using both descriptions and observing that they match. Some criticism also exists, specially because this conjecture was born in the middle of the firewall debate, a scientific discussion which is starting to turn into a real war. Nevertheless, a lot of promising work is arising on the topic (while I was finishing this article, Lenny Susskind uploaded a new work to the arXiv⁴) and future seems to be promising.