Gliomas are the most prevalent subtype of primary brain tumours originating from mutations of the glia cells in the central nervous system. Gliomas are characterized by fast cell growth, strong invasion capability, and well-developed tumour vasculature. Although research and clinical trials have allowed significant progress in the comprehension and treatment of gliomas, they still have […]
In March 2020, a multidisciplinary task force (so-called Basque Modelling Task Force, BMTF) was created to assist the Basque health managers and Government during the COVID-19 responses. BMTF works creating a model based on different approaches: stochastic processes, statistical methods and artificial intelligence. The efforts and challenges to develop a flexible modelling framework able to […]
Preamble In the period 2015-2019, I was hired as a mathematician by a biology department in order to perform a research that eventually would become my doctoral thesis. This text is adapted from the last chapter of that thesis, “Cycles and interactions: A mathematician among biologists” (full text available here ). The symbiosis between mathematics […]
Populations are not static, and the geographic distribution of genetic diversity within and among populations is changing continuously. The drivers of genetic differentiation is one of the cornerstones in evolution, as genetic diversity is paramount for the ability of populations to adapt and persist in changing environments. The spatio-temporal changes in genetic diversity constantly taking […]
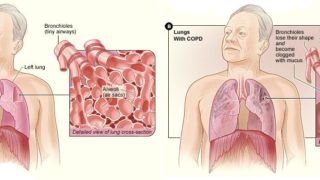
Chronic diseases are already having and will continue to have not only profound economic, social and individual consequences but also a major impact on the use of health resources and design of new care processes. Chronic obstructive pulmonary disease (COPD) is a case on point. COPD is airflow limitation caused by an inflammatory response to […]
Think nothing. Your brain is always on, as your heart, liver or kidneys are, so thinking nothing is the closer you’ll get to a resting state for it, because even when we sleep the brain is quite active. We know that the interactions among different brain regions can be studied with functional magnetic resonance imaging […]
Author: Mikel Lezaun is professor at the University of the Basque Country – UPV/EHU where he is director of the Mathematical Technology Transfer Group Production centers for blood components have the job of supplying hospitals with the products that they need in time and strive to discard as few units as possible due to outdating […]
The Hodgkin-Huxley model for the generation of the nerve action potential is one of the most successful mathematical models of a complex biological process that has ever been formulated. Alan Hodgkin and Andrew Huxley described the model in 1952 to explain the ionic mechanisms underlying the initiation and propagation of action potentials in the squid […]
Renewable energy sources are crucial to react to the continuous increase of energy consumption and pollution by carbon dioxide emissions worldwide. Biofuels, where the energy content is derived from a biological source, are one of the alternatives to oil and natural gas. Still, some biofuels are controversial, like biodiesel, because they imply cultivating certain crops […]
Species distribution models (SDM) are computer algorithms that relate species distribution, occurrence or abundance, with information on environmental conditions and spatial characteristics of locations where the species has been, or is suspected to be, found. These models can be used to predict or to have a better understanding of the species distribution, and are widely […]