Nature cares about the direction time flows: T symmetry breaking measured

Back in the decade of 1950, and inspired by the beauty of the formulation of Quantum Electrodynamics, carried out by Feynman among others in the first half of the twentieth century; scientists thought that all physics had to be invariant under three fundamental symmetries that could relate different physical processes between them. These symmetries were the so called parity, charge conjugation and time reversal.

Parity (P) is the symmetry which relates how space behave under reflection or, talking about physical processes, it implies that the propagation of a particle in a direction should not be affected if we reverse its movement.

Charge conjugation (C) is no more than what its name says: it changes the sign of the charge of the particles so when it acts, for example, on an electron, it changes its charge from -e to +e.

Finally, time reversal (T) implies to rewind the time and see how the processes start to happen from ‘after’ to ‘before’. For instance, the time reversal process of the decay of a pion into a muon and a neutrino is no more than the combination of the result particles to form again the original pion.

These symmetries are very important in the theoretical construction of any physical theory since the combination of them, written CPT, can be shown to be equivalent to the most fundamental symmetry of the nature we know, the so called Poincaré symmetry. Thus, breaking the invariance under CPT is equivalent to breaking Poincaré invariance or else, if we do a trick to conserve it, to having probabilities bigger than one, which is even worse. Therefore, preservation of the combined CPT symmetry is a fundamental property of nature and, since there were no evidences against it, physicists of the first half of twentieth century thought that also the individual symmetries C, P and T were conserved, since that was the simplest way to conserve its product altogether.

But in 1957 it was discovered that there were some processes, associated with the beta decay of a nucleus into another one, that violated the parity symmetry. However this was not a big shock for the scientific community since there was still the hope that the combined symmetry CP, which is the symmetry that relates particles to its corresponding antiparticles, was conserved in order to preserve CPT. But alas, few years later it was discovered that also this symmetry was broken in weak interactions (those carried by W and Z bosons), and also that its violation was needed to explain the most recent cosmological observations that the first machinery born at the light of the space race was providing.

So, in the middle years of the 60’s one thing was clear, CP was broken and also we needed it to be broken, which, since the combined CPT had to be conserved, implied that the most obscure of the three symmetries, time reversal, was also broken by weak interactions and that physics cared about the direction in which the time was flowing. At this point physicists were in trouble. It was kind of easy to measure the amount of violation in the CP symmetry by using the decay of some particles named K and B mesons, but measuring time reversal breaking was a puzzle, since there is impossible to revert time! And this is precisely what a group of the BABAR collaboration was recently ¹ able to measure by doing a very clever trick using the data produced by the B meson factory SLAC (Stanford Linear Accelerator Center – Stanford, USA).

If we would want to measure the level of breaking in the T symmetry, we should find a process in which a particle X decays into another particle Y and compare its rate of production (how common that process is when we put together a bunch of X particles) to the one of the reverse process Y going to X. If there is any difference between both quantities, then the symmetry is not perfect and we can measure how big its violation is just by comparing them. However, as we said before, reversing a process is not, in principle, possible since we cannot reverse time. What physicists of BABAR did to solve this problem was to take advantage of the already known CP symmetry violation in the B mesons produced at SLAC. Specifically, they focused on the decay , whose reverted reaction is , using pairs of entangled mesons to study it.

When a pair of B mesons is produced in SLAC, they enjoy a purely quantum property called entanglement. Simplifying a lot, what essentially happens is that the quantum state of both mesons is completely related, so if we measure one of them and we find it in a particular state, we automatically know in which state the other is. And here the trick is. Since B mesons are violating CP symmetry, the state in which they are (that can be one out of four types named , , and ) is not constant or, in other words, it can oscillate from one to another. This so called flavour oscillation is the main property that allowed the researchers to measure the time reversal process , which would be in principle not allowed if CP and T were conserved.

The experimental procedure is simple when these properties are understood. First, two entangled B mesons are emitted and fly a little time after which their quantum states are measured. Suppose that the entanglement is such that the state of both mesons has to be the same and we find that one of them is in the state. Due to entanglement, we expect the second meson to be also in the state but alas, when we measure it results to be in the state, which implies that there have been a process at some point. So, measuring pairs of mesons and counting how many of them are not in the same quantum state, we have a result for the rate of this concrete process. The other one we need, , can be measured in the same fancy way so when comparing both rates, the final result is a very precise measure (14 sigmas!!) of the time reversal symmetry breaking of weak interactions.

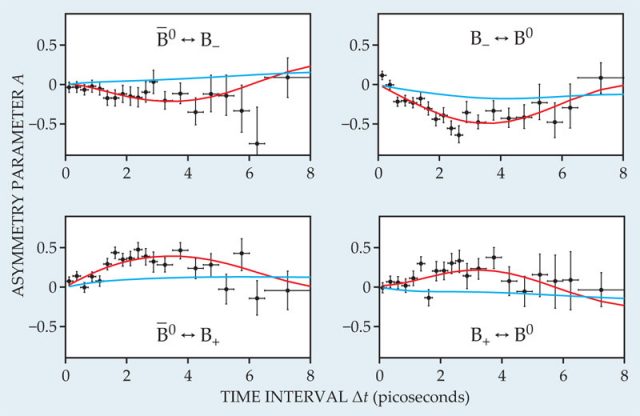
It is important to remark that this is not the first measure we have for this symmetry breaking, but it is the first one to be remarkably precise and no controversial, since former measures could be interpreted in different ways and for long time the scientific community had doubts about if they were dependable enough. This is why the result of Martinez-Vidal et al. is so important. It is the very first precise and dependable measure we have of this property of nature and weak interactions.