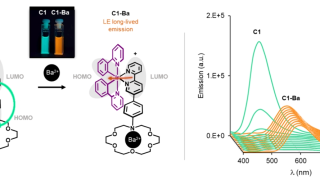
Unlocking the universe’s hidden light: The COCOA Telescope
Astrophysics • DIPC Astrophysics • DIPC Particle Physics • Particle physics
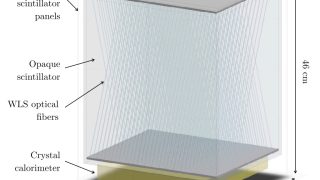
Deep in the heart of exploding stars and colliding neutron stars lies a hidden light we’ve barely glimpsed — gamma rays in the mega-electron-volt (MeV) range. These elusive rays, carrying clues about cosmic explosions and mysterious phenomena like dark matter, have been hard to study due to technological limits. Enter COCOA , a compact, innovative […]