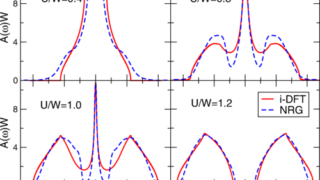
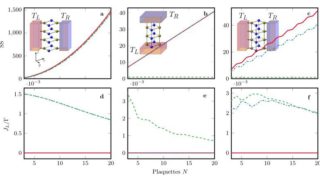
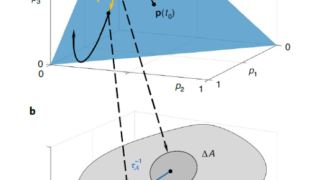
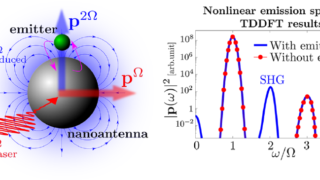
Why Einstein must be wrong
Einstein Authors: Valerio Faraoni, Professor, Physics & Astronomy, Bishop’s University and Andrea Giusti, Postdoctoral fellow, Swiss Federal Institute of Technology Zurich Einstein’s theory of gravity — general relativity — has been very successful for more than a century. However, it has theoretical shortcomings. This is not surprising: the theory predicts its own failure at spacetime […]