Closer to the truth (3): Verisimilitude, seeming, and simulation.

By Jesús Zamora Bonilla February 5, 2025 0 comments Print

For the problem of scientific realism, the most consequential implication of the ‘ugly duckling theorem’ we met in our last entry was that judgments of similarity seem to be not reducible to any kind of algorithmic definition that might tell in an objective way how much ‘similar’ is one thing to another, for these judgments were always dependent on which features of the objects or systems we deem more relevant, and this seems to depend on an arbitrary and subjective choice. The Popperian goal of interpreting the progress of scientific knowledge as a series of theories increasingly ‘more similar’ to the full truth about the world (or about the fragment of the world our theories deal with) would hence collapse under the weight of subjectivism and relativism. If we add the difficulty that philosophers working on the truthlikeness program have had to specify some ways to recognize (by the use of their logical definitions of the concept) whether real historical cases have been examples of ‘approximation to the truth’, then it is no surprise that defenders of scientific realism have preferred to use other types of arguments, instead of the idea of verisimilitude. This can be considered a severe flaw, because it is clear that most scientific theories, laws and models are not literally true, but, at most, simplifications, idealizations, and approximations, and if all falsehoods are equivalent in its lack of truth, then it is better not to analyze science in terms of truth at all, or so it seems.

My own reaction to this predicament was not being afraid by the unavoidably subjective nature of similarity judgments, but happily embrace it, admitting in particular that judgments of the form ‘theory A is more similar to the truth than theory B’ don’t describe an objective property of either theories, but always have a subjective content, i.e., they are the expression of how more or less similar to the truth the theories seem to one particular subject. Veri-simil-itude is essentially a question of seeming. It is always possible that, for a different scientist, it is theory B the one that looks closer to the truth than theory A. After all, as Thomas Kuhn insisted in his famous book The Structure of Scientific Revolutions, science marches by replacing a vision of the world (or ‘paradigm’) with another, and this not only entails a change in which formulas researchers take as the right ones, but also a change of the criteria for deciding when is a formula, a technique, or an experimental method, more appropriate than others.

Under my ‘subjectivist’ approach to verisimilitude, objectivity may be saved not as a kind of transcendental truth, totally external to human subjects, but as a form of intersubjectivity: we can try to show, for example, that under certain specific circumstances some different subjective judgments of similarity necessarily agree. For example, it can be the case that theory A seems more truthlike to scientist X than theory B, whereas the opposite is the case for scientist Y, but perhaps they both agree on the fact that a new experimental result increases the degree in which A seems truthlike (though Y still does not consider this as enough for A surpassing the verisimilitude of B). Stated otherwise: perhaps it is enough (for saving science ‘objectivity’) that scientists agree on some judgments of truthlikeness, especially comparative judgements, and it is unreasonable to demand that they must agree on all of them, comparative and absolute judgements alike.

Another central aspect in which my approach differed from other proposals in the field was in the idea that, once we have dispensed with the goal of defining an objective measure of truthlikeness, we can even go further, and take our definitions not as logical stipulations about what ‘closeness to the truth’ really is (or really means), but as something similar to what we are assuming that scientific theories and conjectures are: not literally true descriptions of an objective reality, but only idealized, distorted, and simplified approximations. In other words, I suggested to see my definitions of verisimilitude as part of a simplified model of science, not as an ambitious attempt to having found ‘the truth’ about it. In my own approach, the idea of verisimilitude is just part of a simulation of the game of science, and as all, simulations, it will be unavoidably partial and caricaturesque. As with most scientific models, they will be useful enough just if they allow to approximately reproduce with easiness (aka ‘to explain’) some aspects we consider to be important of the way science proceeds. I shall leave for the next entry a more detailed account of how my definition(s) of verisimilitude attain exactly this, i.e., a partial reconstruction of ‘the scientific method’. In the remaining of this entry, I just proceed to present the main definition itself.

As I have told, the central idea is replacing the notion of ‘an objective measure of closeness to the full truth’ with a notion like ‘the degree to which a proposition seems closer to the full truth for a particular individual’. One possibility of doing this is by using what Bayesians call a subjective theory of probability: the subjective degree of confidence one subject s attributes to each considered proposition A, p_s(A), being this some number between 0 and 1, which respects the laws of probability (for example, p_s(AVB)= p_s(A)+ p_s(B), if A and B are logically incompatible; or, more exactly, if s knows they are). In the following, I will dispense with the subscript s.

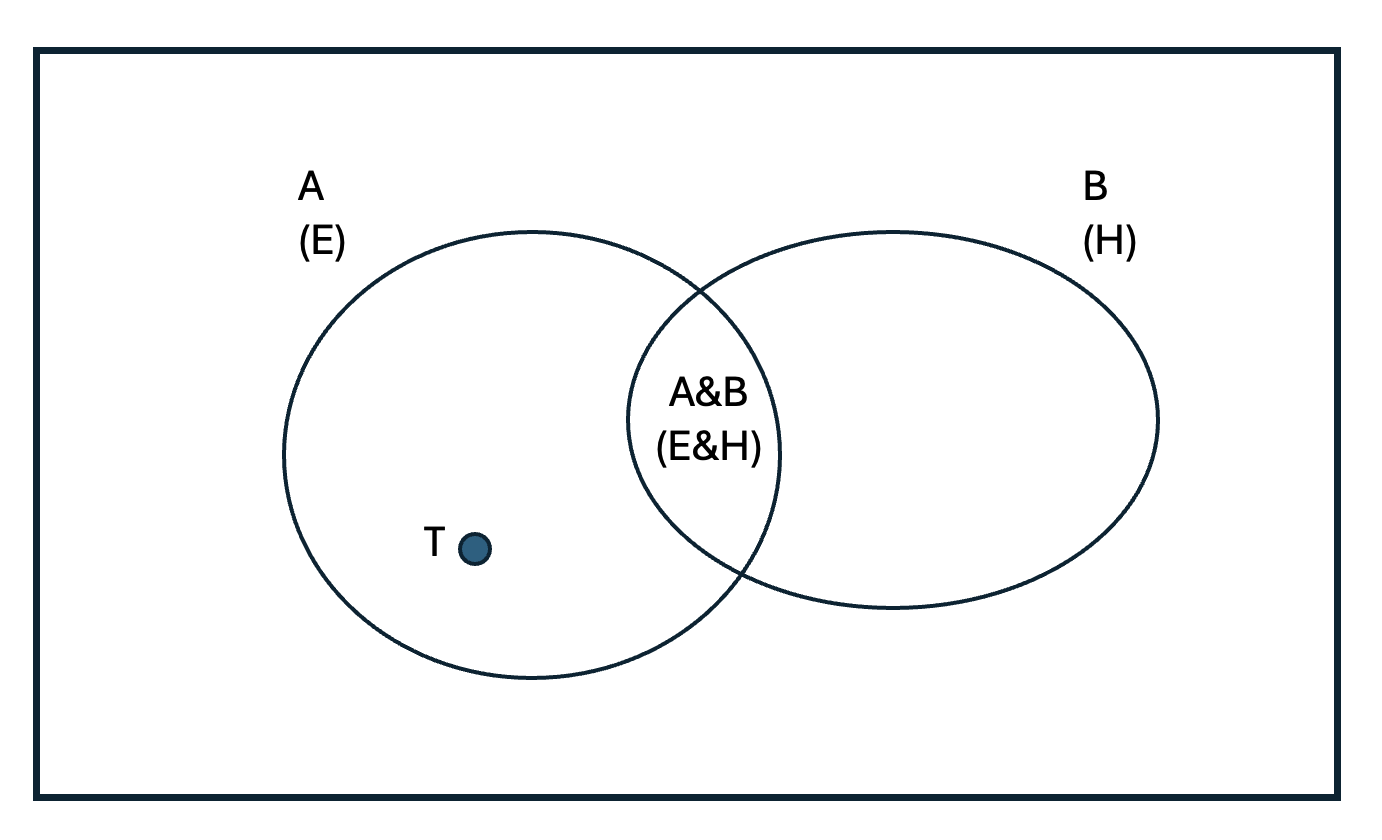
Now, my suggestion is to start with a very simple definition of the similarity that there is for subject s between propositions A and B, or Sim(A,B), as p(A&B)/p(AvB). In the Boolean diagram represented in the figure, this amounts to the proportion between the area of the intersection of A and B, and the area of their union. Another way of expressing it, is as the probability that both A and B have of being true (for s), if at least one of both were true, or p(A&B,AvB). This measure was later identified by other authors as the ‘coherence’ between A and B.

Now enters the truth. Let’s reinterpret A as the empirical evidence E existing about a given scientific question, and B as a particular scientific hypothesis H about the matter. Taking E as empirical evidence entails that we (or our subjects) are assuming that it is true, i.e., that the ‘true state of the world’, T, is one of the states included in the area of E. Well, then I proposed to define the verisimilitude that a hypothesis H has for subject s under the empirical evidence E (or ‘how similar to the full truth H seems to s’) as ‘how similar H is to E for s, weighted by how similar E is to T for s’:

Vs(H,E) = Sim(H,E)xSim(E,T)

= [p(H&E)/p(HvE)]x[p(E&T)/p(EvT)]

= [p(H&E)/p(HvE)]x[p(T)/p(E)] (since T is included in E).

= p(T)*[p(H,E)/p(HvE)]

and, since p(T) is a constant equal for every possible H and E, and since we only want the measure Vs for making comparisons between the verisimilitude of some hypothesis given some evidence for some subjects, we can dispense with the first term, so that, in the end we can stipulate that