The speed of gravity 

Newton’s theory of gravitation assumes that the speed of gravity is infinite and the gravitational interaction is instantaneous. However, Einstein’s theory postulates that it is exactly equal to the speed of light. A team of Chinese physicists lead by Tang Ke Yun, at the Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, China, has measured the speed of gravity with a relative error of about 5% by using Earth tides during three solar/lunar eclipses ¹. The resulting value, between 0.93 to 1.05 times the speed of light, confirms the result postulated in Einstein’s theory. It is expected that new measurements using the same method, but with better gravimeters, could reduce the error by about an order of magnitude.

The Earth tides are essentially the motions in the solid earth induced by the lunar and solar tidal forces. These tidal forces cause a mass redistribution of the solid Earth which results in an additional force. The vector sum of the lunar tidal force, the solar tidal force and this additional force creates a phase lag which can be used to determine the speed of gravity during a solar/lunar eclipse, when the Sun, Moon and Earth are on the straight line observed from a point on the Earth.

The true position of the Sun cannot be observed directly, so the solar tidal force is calculated from its apparent position. Using a formula that incorporates the difference between the time of gravity issued from the Sun and the time of gravity received at ground station, the speed of gravity could be inferred. This time difference has two origins: the first one is the phase lag from the delayed response of Earth to solar tidal force due to its anelasticity and the second one is the time difference caused by the travel speed from the Sun to the ground station, if the real travel speed c_g is different from the speed of light c. Both effects can be incorporated in the formula used in the analysis.

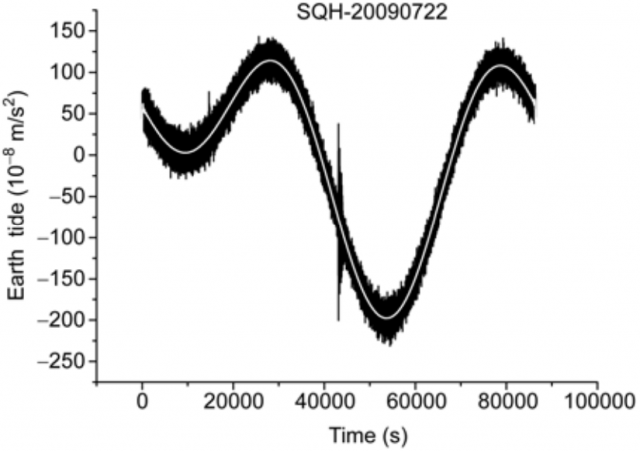
Observational data was recorded July 7, July 22, and August 5 of 2009 by two spring gravimeters coupled to rubidium-clocks located inside the western border of China, very far away from the effect of tides in the ocean: the Shiquanhe (SQH) station in Tibet and the Wushi (WS) station in Xingjiang, China. During these days the phases of the moon are either “new moon” or “full moon,” and the Sun, the Earth and the Moon are almost collinear. A low-pass filter has been used to filter the high frequency disturbances in the signal of the spring gravimeters as shown in Figure 1. The speed ratios of gravity to light are presented in Table 1, resulting in the quoted value from 0.93 to 1.05 for the speed ratio of gravity to light.

The 5% error in the speed of gravity can be reduced in the future by several means. First, the use of either superconducting gravimeters or atom interferometers will reduce the systematic error in the tidal gravity measurements. Second, more data of Earth tide from those stations and the use of additional stations will reduce the statistical errors. And third, other methods for the measurement of the speed of gravity by comparison with the Coulomb speed as proposed by Yin Zhu ², could be used.

For some readers, the use of Newton’s theory instead of Einstein’s one in order to measure the speed of gravity could be surprising. However, the measurement of the speed of gravity by using Einstein’s theory has no meaning, since within general relativity gravity propagates along null geodesics. The speed of light in vacuum, c, and the speed of gravity, c_g, are both determined by exactly the same metric information, hence it is impossible to declare c and c_g to be two separate parameters in general relativity. The only possibility is the use of a post-Newtonian (PPN) theory, a relativistic theory of gravitation using a fixed Minkowskian spacetime which introduces corrections to Newton’s theory by using an expansion in powers of 1/c².

The problem with the use of PPN theories for the measurement of the speed of gravity is that such a test is model dependent, since the speed of gravity enters in the PPN expansion of at the powers of 1/c⁴. The corresponding PPN parameters are known with a large experimental uncertainty and small deviations due to c c_g can be accommodated into a PPN theory with instantaneous gravity waves by properly changing its parameters within current experimental limits. For such a reason, previous claims of the measurement of the speed of gravity ³ has been have been strongly criticized [2].

Finally, let me remark that a direct measurement of the speed of gravity could be obtained after the direct observation of gravitational waves. But, currently, only indirect observation has been obtained using binary pulsars, like PSR 1913+16, whose orbital decay agree at the ~1% level with general relativity (when it is assumed that energy is emitted in the form of quadrupole gravitational radiation). These results yield experimental insights into the speed of the gravitational waves, but cannot result in a direct measurement.