The rhythm of my nerves

Despite the large variety of musical tastes, we all tend to like or dislike certain combinations of sounds. This perception goes down to a basic level when two or more notes play simultaneously, such as in musical chords. A chord is called consonant when it is perceived as pleasant to our ears and dissonant when not. It is not only humans that show preference for consonant chords, but it is a characteristic that extends to all mammals. This distinction between consonance and dissonance forms one of the bases of the western music, but the reason why consonance is favorite to us is still a debated question in perception theory.

Historically, some theories have been proposed to understand the phenomenon. The number ratio theory, attributed to Pythagoras (around 500BC), explains the difference between consonant and dissonant chords on basis of how “simple” the frequency ratio between the tones is. A simple ratio, say a 1/2 frequency ratio of tones separated by an octave, will be perceived as more consonant than the frequency ratio 15/16. In 1877, Helmholtz considered the combined wave of the two tones and explained the sensation as related to the number of shared harmonics by the two frequencies. The more shared number of harmonics between two tones, the more consonant they would sound. These theories, however, do not yet explain the physical basis in the ear of mammals that results in consonant chords perceived as pleasant or harmonious while dissonant chords as unpleasant or inharmonious.

Recently, a group of Russian and Italian researchers have suggested that, rather than an effect derived from the combination of waves, the pleasant sensation might be more related to the processing of the electrical signals by our neuronal system. The team theoretically calculated the output signal from a simple system of neurons, for different combinations of incoming sounds. Their results showed that the output signal from the neurons presented some sort of rhythmical behavior for consonant chords, while not for dissonant chords. A rhythmical firing from the neurons to the brain would be related to a pleasant sensation for us.

To understand the analysis done by the group of researchers, let’s first describe the physical process occurring when we hear a sound. The inner ear of the mammals contains the so called basilar membrane. When a sound reaches the basilar membrane this performs, with good precision, the Fourier transform of the incoming signal. In other words, each position coordinate in the membrane is associated to a frequency of the input sound. The sensory neurons, or simply, sensors, which are responsible for converting the external stimuli into internal stimuli, are directly attached to the basilar membrane. Depending on the physical location of the attachment to the membrane, each sensor will be dealing with one frequency component of the input sound. The signal is then transmitted from the sensory neurons to other neurons along the neural fibers and, eventually, the signal reaches the brain.

The goal of the authors was to characterize the signal transmitted to the brain. By having a description on how the neurons “shape” the output signal towards the brain, it will be possible to determine how this signal looks for different tone combinations.

To simplify the analysis, the authors used a three-neuron system, which is exemplified in Figure 1. Two of the neurons, labeled with N₁ and N₂ in the figure, are sensory neurons, and receive the tones with frequencies Ω₁ and Ω₂. The output from the sensory neurons merges at the input of the third neuron, N₃, which receives the name of interneuron. The output from the interneuron, in turn, is the signal transmitted to the brain and therefore, the signal to investigate.

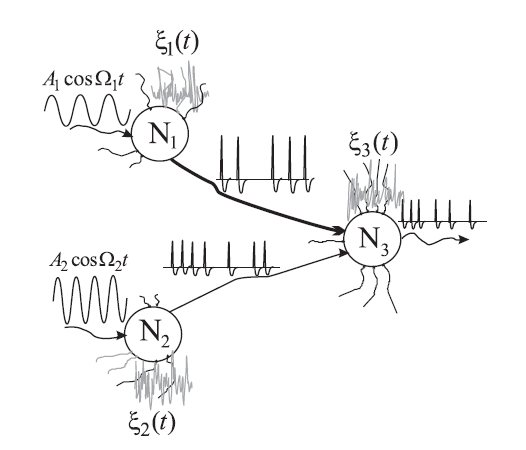
The neurons are modeled with the so called noisy leaky integrate-and-fire neuron model. This model assumes a membrane potential for each neuron. When the input reaches a certain threshold voltage, the neuron fires a spike. An incoming signal results in a train of short pulses from the neuron. The spikes are transmitted from the sensors to other neurons. Applied to the three-neuron system, the input to the sensory neurons is the external sinusoidal signal of frequencies Ω₁ and Ω₂, while the input to the interneuron is the spike train from the sensors, which is received through synaptic connections. In addition, the authors introduce perturbations to all three neurons that represent noise sources from neighboring neurons. The noise signals are represented in Figure 1 with the notation ξ₁(t), ξ₂(t) and ξ₃(t).

For this three-neuron system, the authors studied the spike train at the output of the interneuron, when considering different frequency ratios Ω₁/Ω₂of the input sinusoidal signals at the two sensory neurons ¹. In particular, two cases were considered: small numbers in the numerator and denominators of the frequency ratio (consonant chords) and large number in the numerator and denominator of the frequency ratio (dissonant chords).

It was found that for consonant ratios, the output signal of the interneuron consisted on well-shaped regular peaks while, for dissonant ratios, it was a less regular spike train. That is, a rhythmical and structured spike train fired by the neurons will be perceived as harmonious to us. Thus, the level of regularity gives us a clue to characterize the level of pleasure when listening to a given combination of tones.

In a later work ², the authors propose a way to quantify the regularity of the spike train, by introducing the so called spike regularity measure. The regularity is calculated by using information theory, and quantifies the informational entropy of the spike train from the interneuron: the regularity is higher (smaller entropy), the less random the spike train is. When using this definition, the entropy calculations result, as expected, in a high regularity (very regular spike train) for small natural numbers of the frequency ratios, i.e., for consonant ratios.

This work proposes a way to characterize a sensation by using a physical quantity that can be obtained directly from a spike train by the calculation of its informational entropy. The somewhat vague distinction between pleasant or unpleasant combination of tones can be now mapped precisely to a quantifiable measure.

If the dependency between regularity and pleasant perception as found in this analysis is verified experimentally, the authors suggest the usability of this metric to understand how sounds more complex than musical chords are perceived as pleasant or unpleasant by mammals. The regularity level would be an indicator of the feeling of harmony during sound perception. More interestingly, this quantification does not actually depend on the properties of the incoming signal, but on the nature of the signal processed by the neurons. This suggests the possibility of having a similar explanation of sensations for other senses, not only for sound.