Polarization conserved, counterintuitively

In an electromagnetic wave, the direction of the electric field is perpendicular to the direction of propagation of the wave. We say the wave is circularly polarized if the tip of the vector that represents the electric field describes a circular helix (thus circular polarization is sometimes called helicity) about the direction of propagation. Waves produced by numerous sources are usually not polarized. An incandescent light source, for example, contains millions of atoms acting independently. As there is no correlation between the individual atoms producing the light, the components of the electric field vary randomly.

The phenomenon of absorption and reradiation is called scattering. Scattering can be demonstrated by passing a light beam through a container of water to which a small amount of powdered milk has been added. The milk particles scatter the light, making the light beam visible. Similarly, laser beams can be made visible by introducing chalk or smoke particles into the air to scatter the light. Scattering has an effect on the polarization of light.

If we add up these two phenomena, we can intuitively come to the conclusion that a polarized light being scattered by an optically dense media consisting of particles moving randomly, would result in a randomized state of polarization of the resultant light. We say then that light becomes depolarized. This depolarization has found a lot of applications, from remote sensing to biomedical imaging and diagnostics.

Now, a group of researchers from Materials Physics Center (CSIC-UPV/EHU), DIPC, McQuarie University and IFIMAC, have shown¹, counterintuitively, that the helicity of the incident light can be conserved when it is scattered by an optically dense and random solution of dielectric nanoparticles. They publish their results in Physical Review Letters.

When a nearly monochromatic coherent light (a laser beam) is scattered by an inhomogeneous medium, the resulting optical wave consists of many coherent wavelets. Since de distances travelled by these wavelets may differ by several wavelengths, their interference produce a characteristic pattern of intensity called speckle. Although the study of the statistical properties of speckle patterns has been a topic of high interest during recent decades, the statistics of the polarization of electromagnetic vector waves is still not well understood.

The researchers study a peculiar combination of random samples and laser beams that lead to polarized speckle patterns that exhibit constant polarization regardless of the direction considered. The medium used is composed of “dual scatterers”, meaning that their magnetic (α_m) and electrical (α_e) polarizabilities are identical (they meet the so-called first Kerker condition). In this case, 230-nm silicon spheres become dual scatterers at a wavelength of 1844 nm.

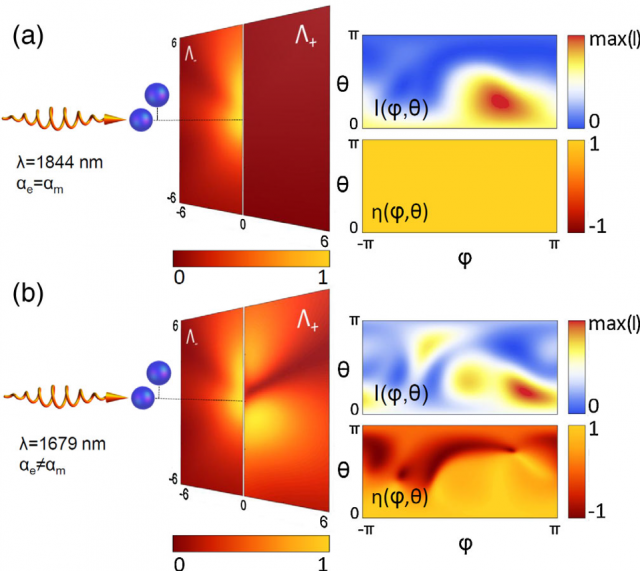
Next, they consider two wavelengths of the incident light: λ = 1844 nm, for which the scatterers are dual, and λ = 1679 nm, at which the scatterers have a dominating magnetic dipolar response, and investigate the scattering of incident helical light on a random distribution of 80 nanoparticles positioned randomly in a cubic volume of 60 μm edge length.

The researchers find (Figure 1) that for 1844 nm, the circular polarization degree η is constant and equal to 1 for any scattering direction, indicating the conservation of helicity in the multiscattering process. For the nondual scatterers, polarization degree does not exhibit any significant preservation of helicity.

These results open a pathway to exploit properties in random scattering media, including intriguing applications in random lasing, as well as to provide new possibilities to characterize magnetic optical properties of nanoscatterers.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.