Topological water waves

In physics, waves often reveal more than meets the eye. A ripple on a pond looks simple enough, but beneath its surface lies a rich mathematical structure that can connect something as everyday as water to the abstract worlds of optics, acoustics, and even quantum mechanics. A recent work ¹ brings this connection vividly to life by showing that water waves can host intricate topological structures—patterns that carry hidden twists and knots—and that these structures can be used to manipulate floating particles in ways reminiscent of “optical tweezers” in light or “acoustic tweezers” in sound.

From simple ripples to structured waves

Ordinary water waves, like those rolling in from the ocean, can be described as plane waves: oscillations that march forward in a straight line, characterized by amplitude, frequency, wavelength, and direction. But when several such waves meet and interfere, the result is no longer a simple ripple. Instead, a structured wave field emerges, with intricate local variations in phase, amplitude, and particle motion. These patterns are not random. They can form robust topological structures—features that persist even if the details of the wave field are disturbed.

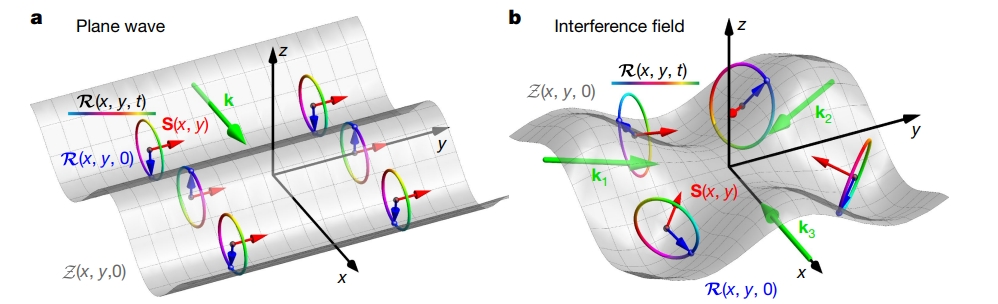
Physicists are fascinated by such structures because they act as the wave equivalent of knots: hard to untie, resistant to small perturbations, and endowed with surprising physical properties. Optical scientists, for example, have long studied light vortices, beams of light that swirl around a phase singularity and carry orbital angular momentum. These beams can twist microscopic particles, trap atoms, or probe the dynamics of galaxies. Acousticians have discovered similar effects in sound. Until now, however, water waves—arguably the most familiar waves of all—had not been systematically shown to exhibit the same topological richness.

Creating topological water waves

In their experiments, the team built precise laboratory wave tanks where multiple water waves could be generated and superposed in controlled patterns. By arranging three plane waves of equal frequency to interfere at specific angles, they produced a hexagonal lattice of *vortices*—points where the surface oscillation vanishes but the phase winds around in full loops. These vortices are classical cousins of the quantized vortices found in superfluids.

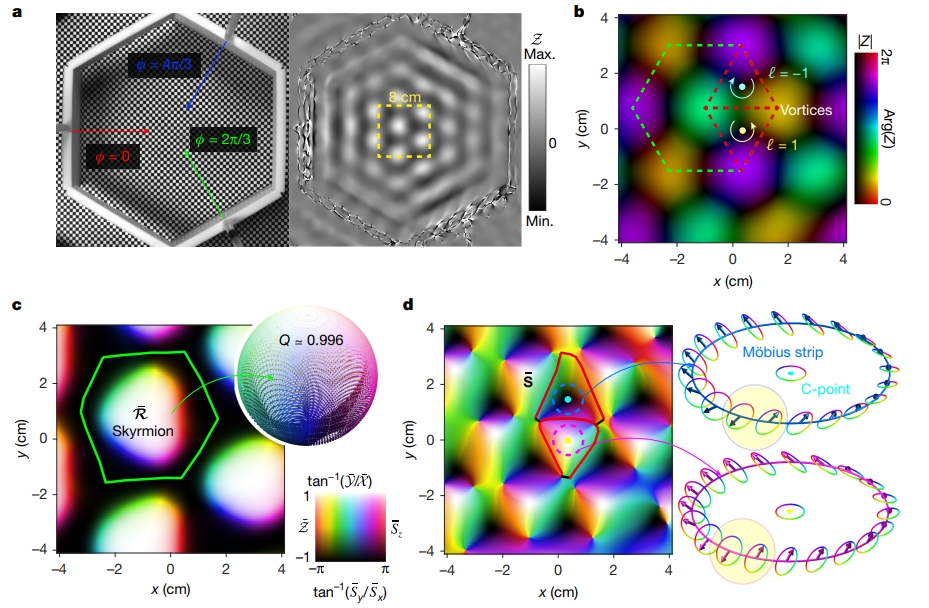
But the story did not end there. From careful reconstructions of the full three-dimensional displacement of water particles, the researchers discovered skyrmions—continuous vector textures where the directions of oscillating particles map onto a sphere, forming topologically protected twists. They also observed *polarization Möbius strips*, in which the elliptical motion of water particles around certain points flips orientation as one makes a closed loop around the singularity, just like tracing the twist of a Möbius band. These phenomena, previously predicted in optics and acoustics, now found a tangible and visually striking counterpart on the water’s surface.

In another set of experiments, the researchers generated circularly symmetric “Bessel-type” water vortices by arranging 24 wave sources around a ring. By carefully tuning the relative phases, they created vortices with different *topological charges*—essentially the number of times the phase wraps around the centre. Higher charges correspond to more complex swirling patterns and quantized angular momenta.

Manipulating floating particles

Perhaps the most striking result came when small floating objects were placed in these structured waves. Just as optical tweezers can hold and rotate microscopic beads with beams of light, water-wave vortices could trap particles, set them into orbit, and even make them spin.

Three distinct forces were at play. First, a gradient force pulled particles toward regions of higher wave intensity, holding them in place. Second, a radiation-pressure-like force, aligned with the momentum of the wave field, drove particles along orbital paths. Third, a torque arising from the local spin density of the water’s motion caused particles to rotate about their own axes.

Experiments with millimetre-sized spheres and even a ping-pong ball showed all three effects in action. Depending on the vortex charge and particle size, objects were stably trapped at the wave centre or along circular rings, orbited steadily due to angular momentum transfer, and spun as though twisted by invisible fingers. Remarkably, the directions of orbital and spinning motion were “locked” together, a feature unique to water waves.

Why this matters

The implications are wide-ranging. First, this research places water waves alongside light and sound as a fully fledged member of the “structured wave” family, capable of hosting topological states with robust dynamics. Second, it opens the door to practical applications. At small scales, structured water waves could provide a new toolkit for microfluidics—the manipulation of tiny droplets, biological cells, or other microscopic entities suspended in liquid. Unlike light or sound, which operate at micro- to millimetre wavelengths, water waves work naturally at the millimetre to centimetre scale, filling a missing range in the spectrum of wave-based manipulation tools.

Beyond the lab, the ideas might even inform our understanding of ocean dynamics. Giant vortices and wave interference patterns in the sea may carry angular momentum and exert forces on floating matter in ways that echo the controlled experiments described here, albeit on a vastly larger scale.

A new wave frontier

This work shows that water, one of the most familiar elements, still holds surprises when looked at through the lens of modern physics. By weaving together concepts from quantum mechanics, optics, and acoustics, the researchers have demonstrated that the humble ripple can be sculpted into vortices, skyrmions, and Möbius strips—and that these patterns can act as powerful tools to control matter.

In doing so, they have not only deepened our understanding of waves but also expanded the playground of topological physics into the most accessible laboratory of all: a tank of water.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.