Topological Quantum Chemistry, the band theory of solids is now complete

Extended and refined by Bloch and others during the 1930s, Bloch’s theory, known as the band theory of solids, accounts very well for the conducting behaviour of materials. When atoms are joined together into a crystal, each of the individual quantum states of the atoms joins with the corresponding states in other (identical) atoms in the crystal to form the various energy bands within the material. The electrons in the atoms then fill up the available states within each band. Topological behaviour arises from the global properties of the band electrons in something called momentum space, a mathematical concept.

But this is a physicist’s point of view, one that considers the crystal as a whole. A chemist, on the other hand, would have a much more local approach where hybridization, ionic chemical bonding and finite-range interactions are paramount. Chemistry, therefore, operates in a real-space (rather than momentum space) description, where atoms and electronic orbitals sit in periodic arrangements.

In any case, and despite the apparent success that the field of new materials has had in predicting some topological insulators, conventional band theory is ill-suited to a natural treatment of topological insulators. One need only look at the paucity of known topological insulators (less than 400 materials out of 200,000 existent in crystal structure databases!) to see the failings of the theory.

Now, a team of researchers from Princeton University, UPV/EHU, Max Planck Institute and DIPC present ¹ a new and complete understanding of the structure of bands in a material and links its topological features to the chemical orbitals at the Fermi level. It is, therefore, a revolutionary theory of Topological Quantum Chemistry, a description of the universal global properties of all possible band structures and materials.

The evolution of a theory

In 1928, just two years after the formulation of quantum mechanics, the German physicist Arnold Sommerfeld modified the classical free-electron model by treating the electrons according to quantum mechanics. But the new theory still contained the unrealistic assumption that the electrons do not interact with the charged lattice ions except to collide with them. As before, Sommerfeld also considered the electrons to be little charged particles of matter.

Beginning in the same year, Felix Bloch, an assistant to Werner Heisenberg in Leipzig, began to make more realistic assumptions in an attempt to formulate a more complete quantum mechanics of electrical conductivity. First, because he wanted to assign a definite momentum and energy to each of the electrons, but not a definite position or a time interval, he chose the wave side of the wave-particle duality. He assumed that the electrons behave, not like particles, but like infinitely extended de Broglie waves. As a result, Bloch did not treat electrons inside metals as a “gas” of particles, but rather as periodic waves extending throughout the periodic crystal lattice. This, it later turned out, helped to explain how electricity can begin to flow in a wire the instant a wire is plugged into a wall socket. If the electrons are viewed as balls of matter, it would take a small amount of time for the current to begin flowing at the rate specified by Ohm’s law.

Bloch made a second assumption. He assumed that the positive metal ions, which are arranged in an infinite, periodic array (that is, in a perfect crystal), each exerts an attractive electric force on the negative electrons. This attractive force formed in visual terms a potential energy that looked like a type of “potential well.” The wells of neighbouring ions then overlapped so that together they formed a periodic arrangement that gave the electron waves a very bumpy ride down the wire.

Bloch then solved the Schrödinger equation for the energies that these types of de Broglie waves (wave functions) could possess while moving in this type of periodic potential. He discovered that the allowed energies of the electrons in the material are joined together into bands of quantum states, just as there are certain quantum stationary states within each atom in which the electrons are allowed to exist. Between the bands, as between the quantum states, there is a range of energies in which electrons are forbidden to exist. The bands in the material are actually created by the joining together of the quantum states of the individual atoms. In fact, if there are a total of N identical atoms in the material, then there are N quantum states within each band. According to a rule in quantum mechanics (the Pauli exclusion principle), only two electrons are allowed to occupy any one quantum energy state of a single atom, and this is allowed only because the two electrons spin on their axes in opposite directions.

Time to incorporate topological insulators

But crystal symmetries place strong constraints on the allowed connections of bands. This is where some crystallographic concepts become handy. In the theory of X-ray diffraction the concept of reciprocal lattice is fundamental, with diffraction patterns being much more related to reciprocal lattices than to real-space ones, even though the former can be defined from the latter. A cell in the reciprocal lattice is called a Brillouin zone, after Léon Brillouin who introduced the concept in 1930.

In this work the researchers first compiled all the possible ways energy bands in a solid can be connected throughout the Brillouin zone to obtain all realizable band structures in all non-magnetic space-groups. Group theory itself places constraints – “compatibility relations” – on how this can be done. Each solution to these compatibility relations gives groups of bands with different connectivities, corresponding to different physically-realizable phases of matter (trivial or topological). The scientists solve all compatibility relations for all 230 space groups by mapping connectivity in band theory to the graph-theoretic problem of constructing multipartite graphs.

Then the researchers developed the tools to compute how the real-space orbitals in a material determine the symmetry character of the electronic bands. Given only the Wyckoff positions and the orbital symmetry (s, p, d) of the elements/orbitals in a material, they derive the symmetry character of all energy bands at all points in the Brillouin zone. To do this general, they extend the notion of band representation (all bands linked to localized orbitals respecting the crystal symmetry), to the physically relevant case of materials with spin-orbit coupling and/or time-reversal symmetry, and identify a set of elementary band representations (EBR).

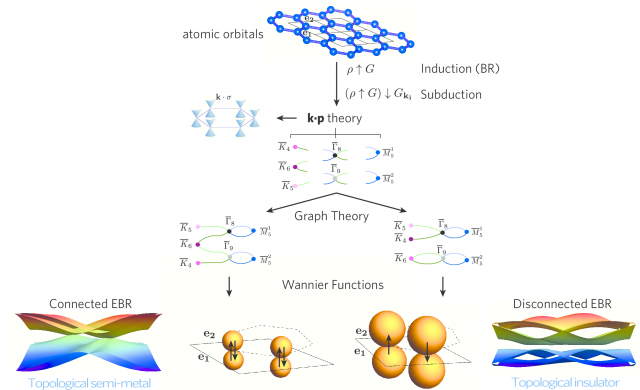
These elementary band representations allow to easily identify candidate semimetallic materials: If the number of electrons is a fraction of the number of connected bands forming an elementary band representation, then the system is a symmetry-enforced semimetal. If, however, the number of connected bands is smaller than the total number of bands in the elementary band representation, then the disconnected bands are topological.

Thus, the researchers were able to classify all topological crystalline insulators. And they show how powerful the method is by predicting hundreds of new topological insulators and semimetals. All these data are now available on the Bilbao Crystallographic Server.

This blend of chemistry and physics is what finally completes the band theory of solids.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.