Optimising production and stock management for blood platelet concentrates

Author:

Mikel Lezaun is professor at the University of the Basque Country – UPV/EHU where he is director of the Mathematical Technology Transfer Group

Blood from donations is separated into three components: red cells, platelets and plasma, and one component or another is then transfused into patients according to their needs. The conditions for storage differ for each component: red cell concentrates can be kept for up to 42 days at temperatures of 1-6ºC. Platelet concentrates (PC) are stored under continuous stirring at temperatures of 20- 24ºC and last just 5 days. Plasma can be frozen to -30ºC and stored for up to a year.

Its short shelf-life, uncertainties regarding day-to-day demand for it and the fact that it admits no delays mean that the production and stock management of PC are hard to adjust. This, in turn, means that stock managers have a natural tendency to overproduce, which leads to high expiration rates. PC are expensive products (with therapeutic doses costing between €300 and €475 each depending on whether they come from platelet pools or from apheresis), so the financial costs of expirations are high.

Faced with this situation, the CVTTH (Basque Centre for Transfusions and Human Tissue) contacted mathematicians at the University of the Basque Country with a view to collaborating on a project to design an IT tool capable of providing objective criteria for decision-making and thus calculating more precisely the number of units of PC to be produced per day.

The model drawn up to manage Basque PC stocks¹ assumes a single stock and disregards any buffer stocks held at hospitals. It further assumes that PC are produced only on working days. The PC produced on Mondays, Tuesdays, Wednesdays and Thursdays join the stock on the morning of the day after production at one day old, while those produced on Fridays join the stock on the following Monday at three days old, thus reproducing the actual operational pattern at the CVTTH. On those days, once expirations have been discounted in the morning and the latest output has been included the manager decides how many units of PC to produce, without knowing how many transfusions are to take place.

The costs of production, storage and supply are not taken into account in the study considered here, and nor is an upper bound on daily PC output. This means that in the model drawn up the daily output is determined by an “order-up-to rule” d_i which is specific to each day i=1,2,…,7 of the week. The value of d_i is an estimate of the number of units of CP that should be held in stock on the morning of a day i to cover expected demand for transfusions up to the incorporation of the stock from the next order after the one for that day. Thus, d₁, d₂, and d₃ must serve to cover all the hypothetical transfusions for Monday-Tuesday, Tuesday- Wednesday and Wednesday-Thursday respectively, while d₄ must cover Thursday-Sunday and d₅ Friday-Monday. The values of d_i are determined based on past records of transfusions given on the same day of the week, with no distinction between ABO/Rh groups.

Output for a working day i of a given week is d_i minus the stock on the morning of that day, plus the expirations up to the time when the next production batch after that day joins the stock. These estimates are obtained using probabilistic and statistical methods based on past records of transfusions. It is reasonable to require that there be a minimum safety stock at the end of each day to guarantee supplies. A fixed output figure is therefore added to the above formula: k₁ for Monday, Tuesday and Wednesday and k₂ for Thursday and Friday. The bigger these numbers are, the greater the stock resulting at the end of each day will be, but the more expiration there will be. The supply policy applied is FIFO (first in, first out), i.e. the PCs that joined the stock first (i.e. those closest to being out-of-date) are supplied first.

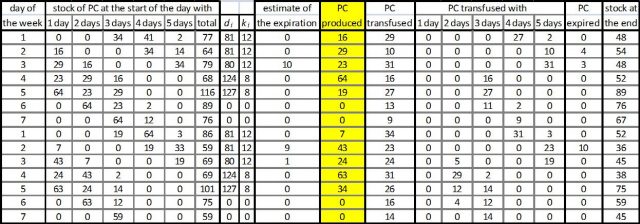
The mathematical model is implemented via an Excel spreadsheet that calculates the day-to-day production, as shown in the figure below. The parameters of the model are defined on the basis of data for 2012. To validate the model a simulation was run using the actual demand from 2013. Taking, for instance, k₁=12 and k₂=8, the minimum daily stock is 15 units of PC and there are 184 expired (2.10% of output, a potential reduction of 85% on the actual figure). Taking k₁=0 and k₂=0 expirations are reduced to 0.75 %, and the minimum daily stock is 3 units.

A mathematical model is always an idealised simplification of a more complex real-life situation. In practice a conservative application of the model has enabled the CVTTH to cut by 40%, thus confirming its potential for substantial financial savings.