Optical transport in disordered photonic materials

A dielectric is a nonconductor of electric charge in which an applied electric field causes a displacement of charge but not a flow of charge. Light propagation through a dielectric medium is determined by the spatial distribution of the material. Photons scatter at local variations of the refractive index. Therefore, how ordered the medium is will have an effect on how light propagates through many everyday and technical materials.

For a periodically organized ordered system, interference dominates light transport and is responsible for optical phenomena in opal gems and photonic crystals.

In disordered ones things vary. A disordered solid is a material that neither has the structure of a perfect crystal lattice nor of a crystal lattice with isolated defects. In a random alloy, for example, the order of the different types of atom occurs, but at random and short-range. Another type of disordered solid is formed by introducing a high concentration of defects, with the defects distributed randomly throughout the solid. In an amorphous solid, such a glass, there is a random network of atoms with no lattice at all.

In random media, transport becomes diffusive through successive scattering events. The characteristic length scale over which isotropic diffusion takes place is the transport mean free path. Materials thicker than the mean free path appear cloudy or white. However, when scattering centers are locally correlated, diffraction effects can be significant. The description of light transport then becomes a challenging problem with many applications, such as the transparency of the cornea to visible light, the strong wavelength dependence of the optical thickness of colloidal suspensions and amorphous photonic structures, and structural colors in biology. Critical opalescence and the relatively large electrical conductivity of disordered liquid metals are closely related phenomena.

For correlated but fully disordered media attention over the last years focused on the emergence of unexpected optical properties like optical transparency and photonic band gaps (groups of wavelengths – bands – that do not propagate through the structure) in 2D and 3D high-refractive-index disordered materials.

The fact is that, currently, there exists no picture that may allow the classification of the different optical transport depending on the structural properties. Now, a team of researchers, including DIPC’s Ikerbasque research professor Juan José Sáenz, makes an important advancement toward solving this fundamental problem ¹. Based on numerical simulations of transport statistics, all relevant regimes in a 2D system composed of silicon rods is identified. The researchers summarize their findings in a transport phase diagram that organizes optical transport properties in disordered media.

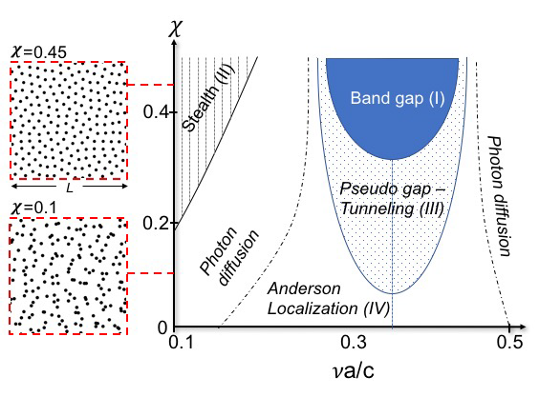
A hyperuniform configuration is one in which the number variance associated with the number of points (particles) in some local observation window grows more slowly than the window volume as the size of the window increases. Thus, hyperuniform disordered photonic materials are disordered, but uniform without specific defects. If we introduce the degree of stealthiness,χ, as the ratio between the number of constrained degrees of freedom to the total number of degrees of freedom, the so-called concept of stealthy hyperuniformity is a measure for the hidden order in amorphous materials

A relatively simple example of a correlated disordered medium is a collection of infinite parallel cylinders of high-refractive index that are distributed according to a 2D stealthy hyperuniform point pattern. This setup provides an ideal laboratory to explore the statistical properties of wave transport in 2D hyperuniform disordered photonic materials.

The numerical results fully support the proposed transport phase diagram in Figure 1 for 2D photonic structures from stealthy hyperuniform point patterns. An important direction for future work is the implications of this phase diagram for electronic transport.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.