Wildfire propagation modelling

Wildfires are a major problem with a strong impact on human life, property and the environment, Global warming and a legacy of poor management are the forces behind the increase in their occurrence and in their magnitude measured in extension. In 2017, an unusual number of extensive and severe wildfires occurred in many parts of the world, including the Mediterranean area, the US and even Greenland. In 2018, almost unprecedented fires devastated large areas of California or Australia. Therefore, it is critical to understand how these fires propagate and which factors affect this propagation if we are committed to prevent their occurrence and, if necessary, to combat them effectively and efficiently..

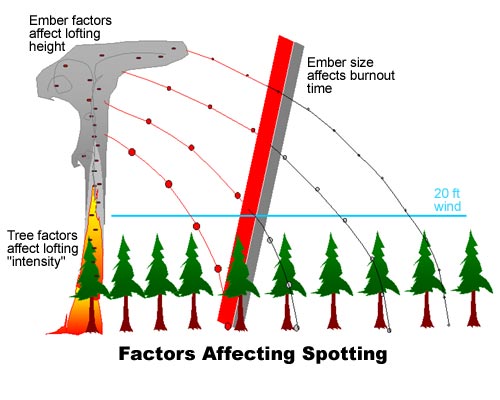
An extremely important phenomenon that may occur during a wildfire is the so-called fire-spotting, i.e., the generation of secondary fires at some distance from the primary fire zone. Spotting may lead to quite dangerous situations both for firefighters and inhabited areas. Any significant understanding of how a wildfire propagates must take spotting into account, even though it complicates the model.

Wildfires are a challenging task for research, mainly because of their multi-scale and multi-disciplinary nature. Now a team of researchers, including Ikerbasque Research Associate Gianni Pagnini (BCAM), Vera Egorova (BCAM) and Andrea Trucchia (BCAM & UPV/EHU), derives a method ¹ based on the idea of splitting the motion of the front into a drifting part and a fluctuating part.

The general movement of the fire front can be considered a closed curve or a surface that is moving with time. This problem can be approached using a level set method. A level set method is a numerical method for representing a closed curve or surface. It uses an implicit representation of the geometrical object in question. It has found widespread use in problems where the closed curve evolves or needs to be recomputed often. A main advantage of the method is that such a representation is very flexible and calculation can be done on a regular grid. In computations where surfaces evolve, changes in the topology of the surface are easily handled.².

A level set of a real-valued function f of n real variables is a set where the function takes a constant value c. For example, the set of all points in an euclidean plane, i.e., n=2 (namely, x, y), that make the function f=x²+y² equal to a constant c, is no other thing than the closed curve we call a circle of radius c.

Tracking the motion of a curve for which every point on the curve is moving in the direction normal to the curve with a given velocity is not a complex problem. Thus, the motion of the fire-front is given by the well known level set equation.

The fluctuating part is more tricky. It has to be the result of a comprehensive statistical description of the physics of the system and should include some random effects like turbulent hot-air transport and fire-spotting. Actually, it is the inclusion of these random effects the real breakthrough in the new methodology the authors propose.

The fluctuating part can have a non-zero mean (for example, due to ember jump lengths), which means that the drifting part does not correspond to the average motion. This last fact distinguishes between the present splitting and the well-known Reynolds decomposition adopted in turbulence studies. Actually, the effective front emerges to be the weighted superposition of drifting fronts according to the probability density function of the fire-line displacement by random effects. The resulting effective process is governed by an evolution equation of the reaction-diffusion type.

The model is suitable for simulating effects due to turbulent convection, such as fire flank and backing fire, the faster fire spread being because of the actions by hot-air pre-heating and by ember landing, and also due to the fire overcoming a fire-break zone, which is a case not resolved by standard models. It has been tested on several fire simulators demonstrating its applicability and effectiveness.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.