The ‘prehistory’ of philosophy of science (3): Introducing Plato

If the preceding post of this series turned out being a little bit disappointing because of the clumsiness and sophistry of the anonymous author of the leaflet we know as On the (medical) science (the first preserved complete work which discusses the nature of a ‘science’, or, in this case, téchnē), we reach today an immensely more gifted and judicious writer, probably one generation younger, and that happens to be the first philosopher from whom complete books have survived: even a lot of books, around thirty, some of them rather thick. I’m talking, of course, of no other than the great Plato (427-347 BC). By the way, the name ‘Plato’ means literally ‘Big-boned’, and it seems to have been his nickname as a wrestler when he was young, his true name being probably ‘Aristocles’. Plato was really a big figure.

Independently of the sympathies or antipathies that you may feel for Plato’s views, the undeniable truth is that Plato is one of the very, very few people (five? ten?) deserving to be considered as true pillars of civilisation. The thought of the previous ‘philosophers’ seems a mere oracular babbling, whereas in Plato’s texts we find the real light, the highest clarity and detail of philosophical arguments, and we find it in a literary form he expressly created, the ‘dialogue’, where flesh-and-blood people talk to each other, and to us, with all the freshness of an amicable conversation. It’s not strange that the Platonic dialogues were copied and recopied, read and devoured so many times during the Antiquity and the Middle Ages, that his written work was preserved more safely than that of any other Greek author. Plato established basically all the areas of what we understand as ‘philosophy’, from ethics to metaphysics, from philosophy of language to politics, from aesthetics to anthropology; perhaps the only big exception is that of formal logic, established by his direct disciple, Aristotle, but as a kind of clarification of what Plato called ‘the art of dialectics’. Of course, epistemology as an explicit branch of philosophical reflection was also inaugurated by Plato, on top of the careless attempts of a fistful of myopic predecessors like the ones we mentioned in the preceding entry.

Before entering into Plato’s ‘philosophy of science’ (epistēmē), it is necessary to recall that his relation to science goes much beyond his own writings, for the Academy he founded served as the most-powerful-to-date centre of research in the ancient world, so much that it is justified to take it as the ‘first university’ in history. In particular, mathematics, astronomy and musical theory are fields in which great advances were made by people working at some moment in the Academy, like Theaetetus, Archytas, Eudoxus and Eudemus. Aristotle himself studied and taught there during the last twenty years of Plato’s life, though his biological work, which we shall consider later in this series, was mainly done after that time. So, Plato had a great concern for ‘the sciences’ (to which he usually refers as tekhnái, or ‘arts’), and promoted a considerable progress in scientific knowledge, the biggest one before the founding, almost one century later, of the ‘Library’ in Alexandria, even if, besides his theories about physics and cosmology that will appear in our next entry, he made little specific contributions to them. In this sense, Plato’s contribution to our understanding of science also has to include the intuition that the most natural and efficient environment for the growth of scientific knowledge is something like what we know today as research centres and scientific communities. He also inagurated the idea that these centres and communities should be supported by the state (though his own Academy wasn’t, but this is the claim we can derive from the description of the ideal state he offers in The Republic), and open to people from different social backgrounds… and even women!, for at least two female members of the Academy are known, Axiothea of Phlius and Lasthenia of Mantinea.

As for Plato’s specific view of the nature of science and knowledge, probably the best explanation he offers is also in The Republic, at the end of book VI, just in the previous paragraphs to those in which (at the beginning of book VII) he presents his definitely more famous ‘myth of the Cave’, of which nothing will be said here. The section I am referring to is known as ‘the simile of the line’, and in it Plato introduces his hierarchical model of ‘degrees of knowledge’. We, the moderns, tend to interpret this expression as referring mainly to differences in the “amount of certainty” each particular theory, proposition or hypothesis has. But Plato’s opinion is rather different. Basically, his claim is that differences among the types of ‘knowledge’ (the difference that there is between a mathematician proving a theorem, and a pair of rascals gossiping in the shadow of the Athenian agora, say) correspond essentially to differences in the types of entities those items of knowledge are about. In a nutshell: ‘better’ kinds of knowledge are ‘better’ because they deal about ‘better’ things. Of course, the ‘higher’ types of knowledge also provide more certainty, but this is secondary, only an accidental sign of the essentially different nature of the things known. The question is, hence, what are these ‘things’? Plato’s answer is given through a visual model, that we are reproducing here.

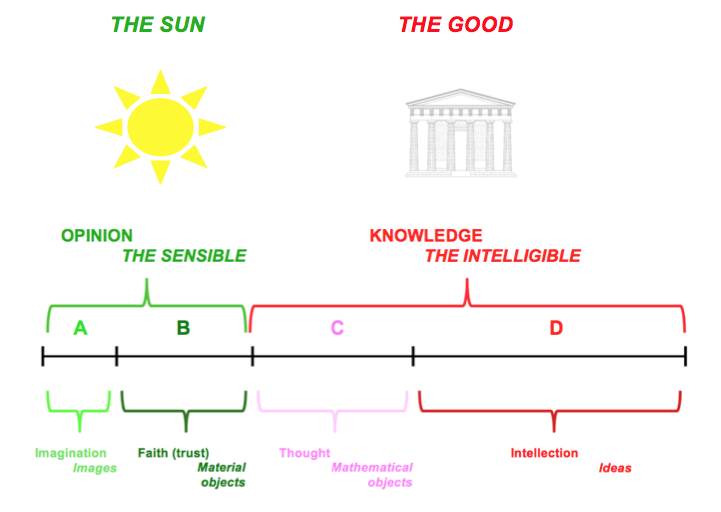
Socrates (the character that in The Republic is explaining this theory to another persona named Glaucon, that in the real world was, equally as Adeimantus, another of the conversants in the dialogue, one of Plato’s elder brothers) invites us to take a line ABCD, and divide it into two unequal segments, AB and CD. One of these corresponds to ‘the sensible things’, those that we can perceive by our senses (more importantly, sight); the other segment corresponds to ‘the intelligible things’, those that cannot be seen, but only thought about (curiously, the text does not decide whether the ‘big’ part is the one that correspond to the intelligible, or it is the small one, but tradition has opted for the representation chosen here). Besides the way in which we perceive or ‘catch’ those different types of entities, another essential difference is that the sensible things are subject to change, whereas the intelligible things are not: they are ‘eternal’. Hence, ‘knowledge’ of mutable, sensible things is what Plato calls opinion (dóxa), whereas that of intelligibles is… well… real knowledge (gnosis), or as we would say, scientific.

Before discussing what those ‘intelligibles’ can be, let’s pause to analyse the next move in Socrates explanation: each segment of the full line must be divided again according to the same proportion. Hence, the segment of the sensible things is divided into two sub-segments, A and B, such that the ratio of A to B is the same as the ratio of AB to CD. This is a metaphor to indicate that the relation between the sensible (AB) and the intelligible (CD) is analogous to the relation between the two kinds of entities that belong to the sensible realm, and which according to Socrates… sorry, to Plato… are the material things B (prágmata) and the images A (éikones, like those in mirrors, calm water, pictures, etc.). This has to be interpreted, obviously, as meaning that the sensible things are a kind of ‘images’ or ‘copies’ of intelligible things, something to which we shall return immediately. Before that, I have just to indicate that, as in the case of the to bigger segments, here there are also two hierarchical different kinds of ‘knowledge’ related to the two types of entities or the two types of ‘epistemic achieving’: to images it corresponds imagination (eikasía), whereas to material things it corresponds faith (pistis), which, in Plato’s times, is ‘faith’ not in the religious sense of ‘believing in the miraculous’, later associated to the spread of Christianism, but in the wider sense of ‘trusting without an absolute proof’, or ‘pragmatic belief’ (we are talking about prágmata, after all). This pistis is perhaps more similar to what some philosophers of science known as ‘the natural ontological attitude (NOA)’, that of accepting acritically the existence of the things surrounding us, or to the ‘Lebenswelt’ or ‘being-in-the-world’ of phenomenologists like Husserl or Heidegger.

The moral of all this is that, according to Plato, there is no science of the material things, only ‘opinion’, opinion that, in the best of the cases, is something that we trust, but acritically, without sufficient reason. After all, imagination (of which dreams would be a paradigmatic example) is, more clearly still, not ‘science’ or ‘knowledge’ at all. What Plato is telling us is, hence, that ordinary knowledge of the material world is just a kind of ‘dream’, or, more precisely, that it is to real science no more than what dreams are to wakefulness.

‘Socrates’ proceeds then to divide the other segment of the line according to the same proportion, so that C is to D as A is to B (or as AB is to CD). C corresponds to mathematical entities (the examples mentioned by Plato are actually geometrical entities: the circles, lines, etc., mathematical theorems speak about; he does not mention numbers, what may lead us to ponder whether he would have placed these into C or into D). Lastly, the inhabitants of D are… you correctly guessed it: what we know as ‘Platonic Forms’ (éidē, singular éidos), or what in most other languages than English are known as ‘Platonic ideas’ (éidos means literally the ‘aspect’ or ‘(visual) shape’ of something, and comes from the same Indo-European root as latin video, ‘I see’; idea also derives from éidos, with basically the same meaning in Greek). ‘Form’, in Greek morphē, is probably a translation Plato himself wouldn’t have approved, though, as you know, was the term of choice for Aristotle to describe something similar, that we shall encounter later in this series. In fact, there is a deep reason for rejecting that translation, one that is easy to see when we examine the relation between C and D: mathematical objects like triangles, the inhabitants of C, have, obviously, a spatial form, a shape, but D, the highest realm, does not contain ‘triangleS’, but, instead, it contains the essence of triangularity, that in which being a triangle consists, what we think about (but do not see) when we think about a figure that it is a triangle. This essence is the ‘Form’ of triangle, but not in the sense of having this geometrical form (an equilateral one, say), or that form (a scalene triangle, for example), but in the sense the most abstract and universal definition or understanding of triangularity.

So, if C is to D as A is to B, this means that specific triangles are also like copies of ‘the Triangularity’, and this also means that the kind of knowledge that we might attain of mathematical entities is not as ‘pure’ as the knowledge we may have of the Forms: ‘thought’ (‘discursive thought’, or ‘thinking step-by-step’, would be better translations of diánoia) is like a kind of ‘dream’ as compared to ‘intellection’ (nóesis). Probably because of this, Plato refers to the ‘sciences’ belonging to the segment C as tékhnai, ‘arts’: mathematics, astronomy and music (the two last ones not being ‘empirical’ astronomy and music, but their ‘theoretical’ counterparts, a topic to which we shall return in the next entry). The only real science (epistēmē) mentioned in the relevant paragraphs of The Republic is what he calls ‘dialectics’, or ‘the dialectical science’ (dialektikē epistēmē), which is a curious name for a science, of course: ‘dialectics’ means simply ‘the art of dialogue’, i.e., knowing how to argue. Plato elevated this ‘technique’ to the noblest position in his scale of science, as something like ‘the understanding of the logical relations between some Forms and others’. But there seems to be a tension between what he reproaches to geometry so that it can not be the ‘purest’ science (i.e., that it proceeds step-by-step, in an argumentative fashion, taken for granted assumptions that later we shall see named as ‘postulates’, in Greek axiómata), and the fact that the purest science is for him the art of dialoguing, which also occurs essentially step-by-step (the prefix dia– has this precise meaning both in dialektikē and in diánoia). Perhaps he is mixing here the process of dialectics with its goal, which would be the intellection of the pure Forms, something like the aha! moment we might experience when we understand something… or rather, when we understand everything, for understanding something consists in understanding its relations to everything else, so it is not possible to have a ‘complete’ understanding of a ‘portion’ of reality.

In a nutshell, Plato’s view of ‘the sciences’, the first systematic theory we have about what they are and how they are attained, consists in proposing us a kind of scale of knowledge, from mere dreams to more or less solid opinions about material things, to cleverer mathematical constructions and demonstrations (all of which only merits for him the qualification of ‘arts’), and finally, to the only thing that would deserve to be called ‘science’: the deepest understanding of ‘the Totality’, which belongs into an ontological realm of eternal things, compared to which the material world in which we live is nothing but an absurd dream, a flawed image, a blurred shadow. Of course, you may be wondering what the two icons on the top of the figure (the Sun and the Good) may be standing for… but this will be the matter of our next entry.