The essential physics of the Mott metal-insulator transition at negligible computational cost

Density functional theory (DFT) is a theoretical treatment of molecules in which the electron density is considered rather than the wave functions of individual electrons. In other words, it is a way of describing many-electron, in general, many-fermion, systems in which the energy is a funtional of the density of electrons (fermions).

DFT is without doubt one of the most popular and successful approches for the description of matter with important applications in condensed matter physics, material science and computational chemistry. DFT owes its success to its relative simplicity and low computational cost as compared to other approaches for solving the quantum many-body problem. Despite its simplicity, DFT is in principle exact, that is, it can provide the exact ground state energy and density of many-electron systems. In practice, of course, an approximation for the exchange correlation energy functional is needed and a plethora of such approximations have been suggested.

However, standard wisdom has it that density functional theory is not capable of describing strongly correlated materials.

The origin of this misconception is twofold. The Kohn–Sham equation is a Schrödinger-like equation of a fictitious system, the “Kohn–Sham system” (KS), of non-interacting particles (typically electrons) that generate the same density as any given system of interacting particles. The Kohn–Sham equation is defined by a local effective (fictitious) external potential in which the non-interacting particles move called the Kohn–Sham potential. By construction, the exact exchange-correlation (XC) potential of the KS yields the exact electronic density and directly related quantities. However, approximations to the XC potential often miss step features that are crucial ingredients to capture strong correlation effects in diverse physical situations due to the derivative discontinuity of the generating XC energy functional. Features such as molecular dissociation, fermion gases in optical lattices, or transport.

On the other hand, the interpretation of the KS excitation energies as true excitation energies is not rigorously justified, even if the exact XC potential is used. While in the limit of weak correlations this may be a reasonable approximation, it completely fails in the opposite limit. In general, extracting excitation energies in a DFT framework is not straightforward. While charge neutral excitations are accessible via time-dependent DFT, excitations which do change the number of electrons such as those probed in (inverse) photoemission are encoded in the spectral function, an arduous quantity to calculate also for time-dependent DFT. Dynamical meanfield theory combined with DFT offers a pragmatic approach to compute the spectra of strongly correlated materials, although the associated double counting problem remains unsolved.

Recently, a method has been proposed to compute the spectral function ¹ of a nanoscale tunneling junction using an extension of DFT, called steady-state DFT or i-DFT. In i-DFT the fundamental variables are the non-equilibrium steady-state density of and current through the junction. Hence, the KS system requires a non-equilibrium extension of the standard XC potential as well as the introduction of an XC contribution to the applied bias in the electrodes. In an idealized scanning tunneling microscope (STM) setup where one of the electrodes (i.e., the “STM tip”) couples only weakly to the nanoscale junction, the spectral function at frequency can be obtained from the differential conductance.

Now a team of researchers generalize ² the i-DFT+STM approach to calculate the spectral function of arbitrary bulk systems.

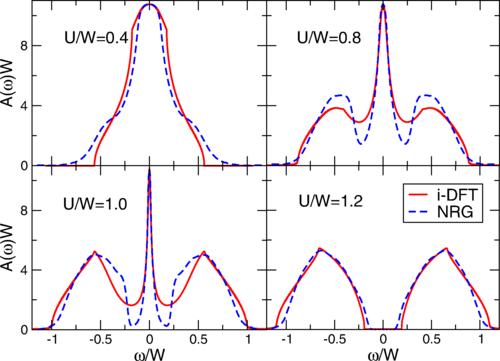
Metal–insulator transitions (MI) are transitions from a metal to an insulator. These transitions can be achieved by tuning various ambient parameters such as pressure or, in case of a semiconductor, doping. Materials exhibiting a transition between a metal and an insulator were extensively studied by Nevill Mott, after whom the interaction-driven insulating state is named. The Hubbard model is one simple model commonly used to describe metal-insulator transitions and the formation of a Mott insulator.

The researchers show that the Mott metal-insulator transition in the Hubbard model, one of the main paradigms in the field of strongly correlated electrons, can be described by i-DFT provided that both the XC potential and the XC bias feature steps as function of the steady density and current. The authors illustrate the MI transition in two different crystal structures, the Bethe and the cubic lattices.

Importantly, the i-DFT spectra capture the essential physics of the Mott metal-insulator transition at negligible computational cost, paving the way to an ab initio description of strongly correlated solids within a density functional framework.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.

Disclaimer: Parts of this article might have been copied verbatim or almost verbatim from the referenced research paper.