Polariton anomalous Hall effect in transition-metal dichalcogenides

Two-dimensional materials, such as transition-metal dichalcogenides embedded in optical cavities, stand out as an excellent platform where strong light-matter interactions can be studied. Moreover, their band structures bring about nontrivial topological features, including the possibility of inducing some really interesting ones, like the polariton anomalous Hall effect.

But, before getting into that let’s go through some basic concepts concerning light-matter interactions.

An exciton can be described as an electron-hole pair in a crystal that is bound in a manner analogous to the electron and proton in a hydrogen atom. Thus, the exciton behaves like an atomic excitation that passes from one atom to another. Exciton energy states involve a band with a particular dispersion law that depends on the crystal properties. But, how are excitons created in the first place? In most cases excitons are induced by an electromagnetic wave, a photon. So the more correct name for the resulting exciton in these cases would be photoexciton.

Interestingly, in some cases the frequencies of vibration of the incoming electromagnetic wave and the resulting exciton are very similar, and they resonate. When they have a strong resonance interaction with each other a quasi-particle results from the admixture of states of the photon and the exciton. This is a polariton.

Let’s add now some more brief concepts about topological insulators.

Topological insulators are electronic materials that have a bulk band gap like an ordinary insulator but have conducting states on their edge or surface. The conducting surface is not what makes topological insulators unique, but the fact that it is protected due to the combination of spin-orbit interactions and time-reversal symmetry.

Researchers are chasing efficient ways to break this time-reversal symmetry without using an external magnetic field, though. Actually, what they are trying to achieve is the realization of the quantum anomalous Hall effect, a quantized version of the anomalous Hall effect.

And finally, let’s introduce the concept of Berry curvature. A Berry phase is a phase that can appear in the wave function for a quantum-mechanical system that depends on various parameters when parallel transport is performed in the so-called parameter space, the set of all possible combinations of values for all the different parameters. The Berry curvature is the gauge field associated with the Berry phase.

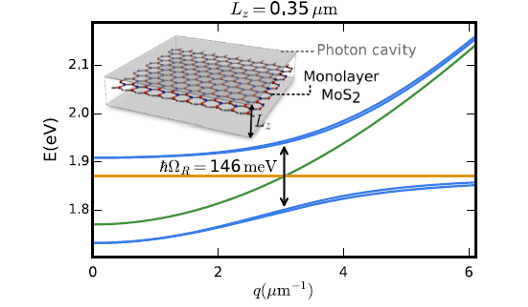
Now, a team of researchers from different institutions, including DIPC, has studied ¹ strongly coupled excitons and photons in a monolayer of MoS₂, a transition-metal dichalcogenide, embedded in a cavity. They have focused on the role of the composite Berry curvature, arising from both the bare constituents – excitons and photons – and their coupling – the polariton, on the motion of the composite excitations, and the possibility of inducing a polariton anomalous Hall effect.

The researchers find that the cavity size promotes a selection-rule breaking. The coupling results in a splitting of the polaritonic branches and a strong enhancement of the polariton Berry curvature, much beyond their constituent contributions. Interestingly, the polariton Berry curvature peaks in the strong-coupling regime what would give rise to a polariton anomalous Hall effect.

This results need to be checked experimentally. Actually, the researchers believe that the generation and observation of polaritonic wave packets are already at experimental reach. Techniques like optical injection with laser beams and polarized short pulses, direction-controlled ballistic ejection from condensates provide very localized wave packets, with micron-scale propagation lengths, and trajectories that can be tracked in real time.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.