Few-mode quantum description of any electromagnetic spectral density

When you first study electromagnetism, all the electromagnetic waves you find are plane ones, waves in which the electric and magnetic fields are both orthogonal to the direction of travel of the wave. But this is a mode – the field pattern of the propagating wave – that is somehow ideal, as it exists in free space far from any antenna. In other environments much more modes are possible.

In a nanophotonic setting, many modes exist, with very different properties, but also their mutual couplings are present. Since it is interesting the use of nanophotonic devices for quantum optics and quantum technology applications, there is large interest in developing strategies for quantizing electromagnetic modes.

Take the case of hybrid metallodielectric setups, designed with the aim of combining the strong field confinement and enhanced light-matter interactions of plasmonic resonances with the long lifetime of microcavity or photonic crystal modes. Standard ways of obtaining quantized modes are not valid here.

While macroscopic quantum electrodynamics provides a framework for such quantization in material structures described by electromagnetic constitutive relations, it describes electromagnetic fields by a continuum of harmonic oscillators, restricting its applicability to cases where they can be treated perturbatively or eliminated by Laplace transform or similar techniques. New models are, thus, needed; preferably, models using only a few electromagnetic modes.

The interaction of a single emitter with an arbitrary electromagnetic environment can be fully described by the spectral density – a function describing how energy is distributed among frequencies, obtained from classical electromagnetic calculations, which encodes the electromagnetic mode density and emitter-mode coupling. Now, a team of researchers has produced ¹ a simple and easily implementable framework for obtaining a few-mode quantum description of any given spectral density.

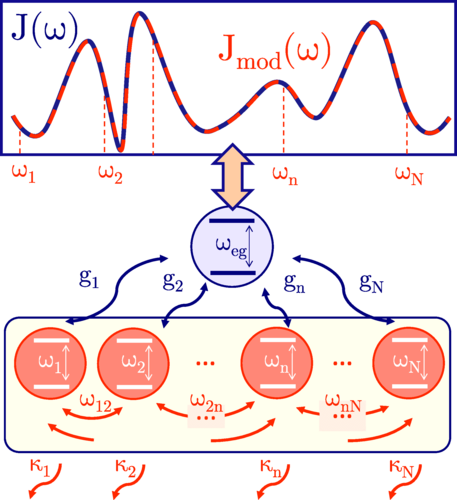
Starting from macroscopic quantum electrodynamics, the new model system consists of a discrete number of interacting modes coupled to independent flat background baths. Fano diagonalization, originally developed for autoionizing states of atomic systems, then provides a compact form for the model spectral density which can be fitted to any level of accuracy to the full spectral density of the interaction obtained from Maxwell’s equations.

The researchers checked the power and validity of this procedure in a hybrid structure comprising a plasmonic nanocavity and a high-refractive-index microresonator. The few-mode model retains the information about the full environment, as accurate calculations of far- and near-field observables show. In other words, it is possible to construct and parametrize a few-mode master equation that accurately describes the interaction of a quantum emitter with the original electromagnetic environment.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research papers.