On-demand spectral response of phonon polaritons in van der Waals materials

In the quantum theory of many-body systems, collective oscillations are called collective excitations. In a quantum context, everything is quantized. Hence, collective excitations become quantized modes because of the cooperative motion of the whole system as a result of interactions between particles. They may be electronic excitations in atoms and are referred excitons.

In most cases, as excitons are induced by an electromagnetic wave, a photon, they are called photoexcitons. If we now consider an electron missing, a hole, a proton lookalike, an exciton can be described as an electron-hole pair in a crystal that is bound in a manner analogous to the electron and proton in a hydrogen atom. Thus, the exciton behaves like an atomic excitation that passes from one atom to another. Exciton energy states involve a band with a particular dispersion law that depends on the crystal properties.

Interestingly, in some cases the frequencies of vibration of the incoming electromagnetic wave and the resulting exciton are very similar, and they resonate. When they have a strong resonance interaction with each other a quasi-particle results from the admixture of states of the photon and the exciton. This is a polariton. In this case there is no longer a sharp difference between the excitons and the photons in the crystal; hence, the speed of light through the crystal depends on the frequency, a characteristic of polaritonic substances.

Thus, polaritons are quasiparticles resulting from the strong coupling of photons with a dipole-carrying excitation.

On the other hand, atoms are bonded to other atoms in the crystal . Rather than being independent of one another, the vibrations of adjacent atoms are coupled by virtue of the atomic bonding. These vibrations are coordinated in such a way that travelling lattice waves are produced. The thermal scattering of free electrons during electronic conduction is by these vibrational waves, and these elastic waves also participate in the transport of energy during thermal conduction. These vibrational waves are sometimes called phonons and they are a dipole carrying excitation. Phonon polaritons result from the coupling of an infrared photon with an optic phonon.

In recent years, phonon polaritons with extraordinary properties have been discovered in polar van der Waals crystals. Two examples are dielectric hexagonal boron nitride, where such exotic phenomena as ray propagation or hyper-lensing effects can be observed, or the semiconductor α-MoO₃, which reveals in-plane anisotropic propagation with ultra-low losses, offering opportunities for the development of a planar directional control of light–matter interactions at the nanoscale.

However, despite the extraordinary properties of these phonon polaritons in van der Waals crystals, there is still an important technological drawback for their implementation into nanophotonics technologies, namely the narrow and material-dependent spectral band where they exist (the so-called Reststrahlen band, defined between the transverse and longitudinal optic phonon frequencies). A broad spectral tuning of a Reststrahlen band in a polar van der Waals material, and consequently of the phonon polaritons supported within it, does not exist.

Now, a team of researchers shows ¹ that intercalation is an efficient route to spectrally tune phonons polaritons in a van der Waals crystal, the metal oxide α-V₂O₅.

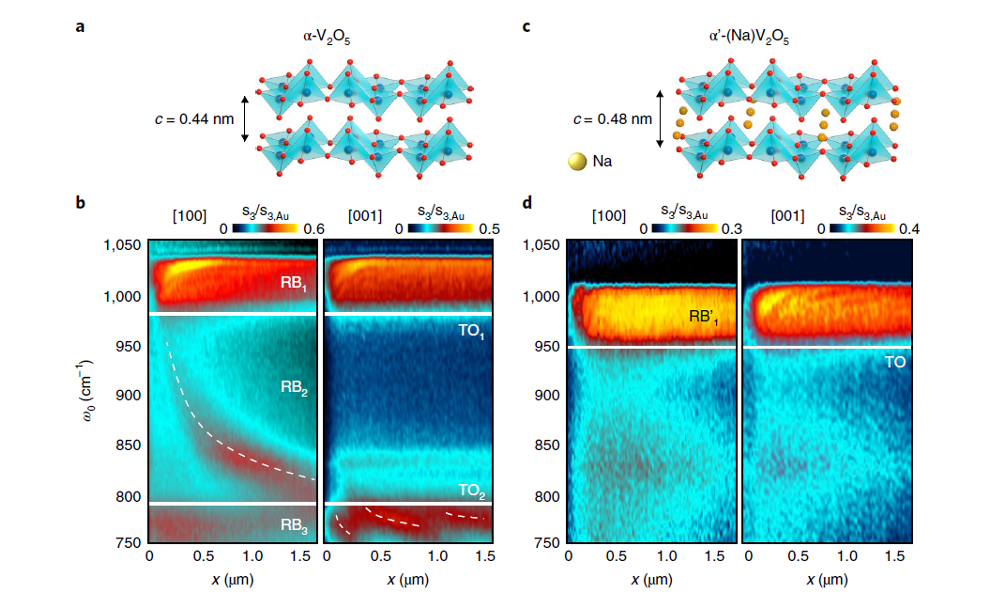
By near-field imaging of Na-intercalated α-V₂O₅ (forming the crystal α’-(Na)V₂O₅) the researchers find a shift equivalent to a 60% of the initial width in the Reststrahlen band, and consequently of the phono polaritons supported within it. Phonons polaritons in the intercalated α’-(Na)V₂O₅ crystal exhibit ultralow loss (lifetimes of 4 ± 1 ps) and in-plane anisotropic propagation, similar to phonons polaritons in pristine α-V₂O₅ (lifetimes of 6 ± 1 ps), evidencing that the intercalation of atoms in between the van der Waals crystals layers does not substantially affect the polaritonic properties of the crystal.

Considering that a large variety of ions and ion contents can be intercalated in layered materials, on-demand spectral response of phonon polaritons in van der Waals materials can be expected, eventually covering the whole mid-infrared range, something critical for the emerging field of phonon polariton photonics.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may be copied verbatim or almost verbatim from the referenced research paper.