A new approach to covariate shift adaptation

In probability theory and statistics, a collection of random variables is independent and identically distributed (iid) if each random variable has the same probability distribution as the others and all are mutually independent. Most supervised machine learning methods assume that training and testing or production samples are drawn iid from the same underlying distribution. But reality has its ways and covariate shift often occurs.

Covariate shift, also called data shift, is a situation in which the distribution of the model’s input features in testing or production changes compared to what the model has seen during training and validation. In such scenarios, conventional supervised classification methods can perform poorly due to the risk of operating near the system’s limits.

An example would be a collection of consumer behaviour data for a certain population, like a large city. The training was done in a certain period of time that corresponded to certain demographics. Some time later, demographics has changed due to, say, an ageing population, migrations or other economic factors. Consequently, the consumer behaviour distribution has shifted, we face a covariate shift, and we need to prepare our learning method for this eventuality.

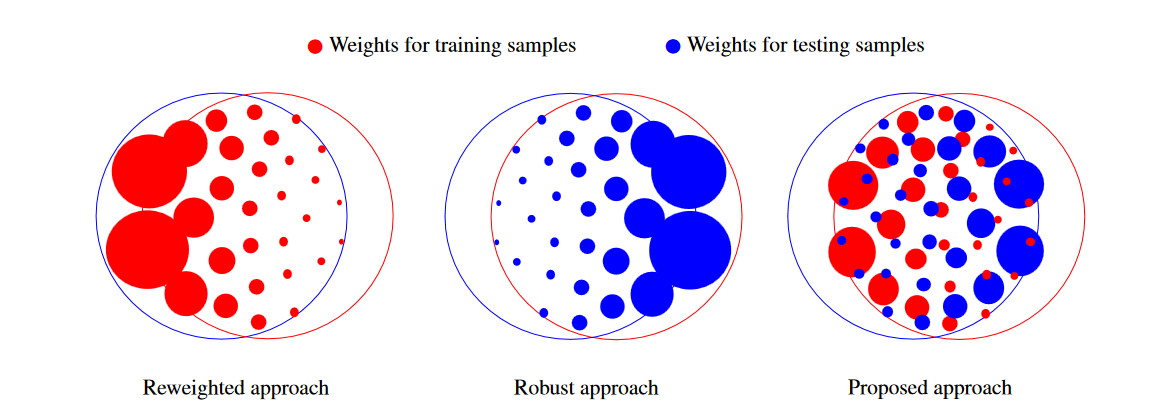
Two main approaches exist to covariate shift adaptation. Most of the existing methods are based on the reweighted approach. These methods weight loss functions at training using the ratio p_te / p_tr (where p_tr and p_te are the marginal distributions of instances of training and testing samples), so that training samples more likely in the test distribution are assigned higher weights, increasing their relevance at training.

On the other hand, robust methods are derived from a distributionally robust learning framework, where the feature expectation matching constraints are obtained from training samples, but the adversarial risk is defined on the test distribution. Such methods weight feature functions at testing using the ratio p_tr / p_te .

Both approaches yield poor results if the respective ratios are high for certain training or testing, variables. As in practice, the distributions of training and testing instances can differ in an arbitrary manner, now, a team of researches proposes ¹ a learning methodology that can tackle such general covariate shift and addresses the limitations of existing approaches by weighting both training and testing samples, what the team calls double-weighting approach.

The methods proposed are based on minimax risk classifiers and utilize weighted averages of training samples to estimate expectations of weighted feature functions under the test distribution. The researchers then proceed to experimentally assess the performance improvement obtained in multiple covariate shift scenarios.

The experimental results show that the proposed method provides improved adaptation to general covariate shifts, even in situations where the supports of training and testing samples are not contained in each other, over existing methods.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article might have been copied verbatim or almost verbatim from the referenced papers.