New linear optics of particle accelerators using Moebius transformation

Author: Victor Etxebarria, professor, Dept. Electricidad y Electrónica. Fac. Ciencia y Tecnología, Universidad del País Vasco-UPV/EHU

The propagation of light -observed and governed since ancient times by simple lens construction- has long been described through classical geometrical optics. However, in particle accelerators we do not transport photons but beams of electrically charged particles subjected to repulsive forces that tend to unpack the particle beams. Optics of particle accelerators require electromagnetic lenses to bend, drift, focus, defocus and correct chromaticity of particle beams in directions x and y transversal to their transport direction z.

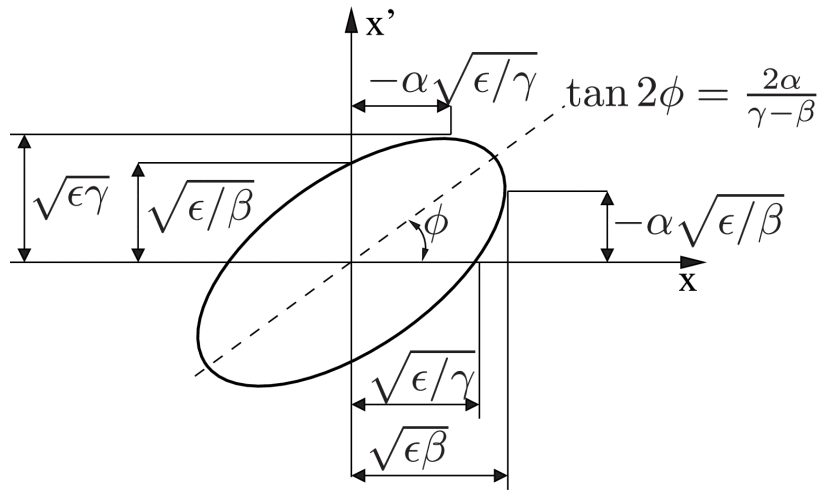
Beam lines in an accelerator are represented by plotting in phase space the coordinate x and conjugate momentum p_x of a particle after each pass through a unit cell, leading to an ellipse whose shape is described through the classical Twiss parameters as shown in Figure 1.

Instead of using the classical beam line space, we have proposed a complete new complex formalism of the linear beam dynamics ¹. By using the complex domain, we have obtained and solved a general differential equation, which has led us to the remarkable finding that the general complex transformation of a linear beam line is a Moebius transformation. This kind of geometrical transformation can be extended to the Riemann sphere, and Moebius transformations form a group, meaning that the composition of Moebius transformations is a new transformation in the group. This important finding implies that if each single beam line cell is described by a Moebius transformation, the whole line is described by a Moebius transformation as well.

Common electromagnetic lenses in linear and circular accelerators must be combined to obtain compound cells to control the beam both in the x and y transversal directions. For instance, focus-defocus (FODO) units require at least two quadrupoles, since focusing one direction defocuses the other one. In general, beam lines are designed to control and stabilize their particle transport as close as possible to the best nominal trajectory in both directions.

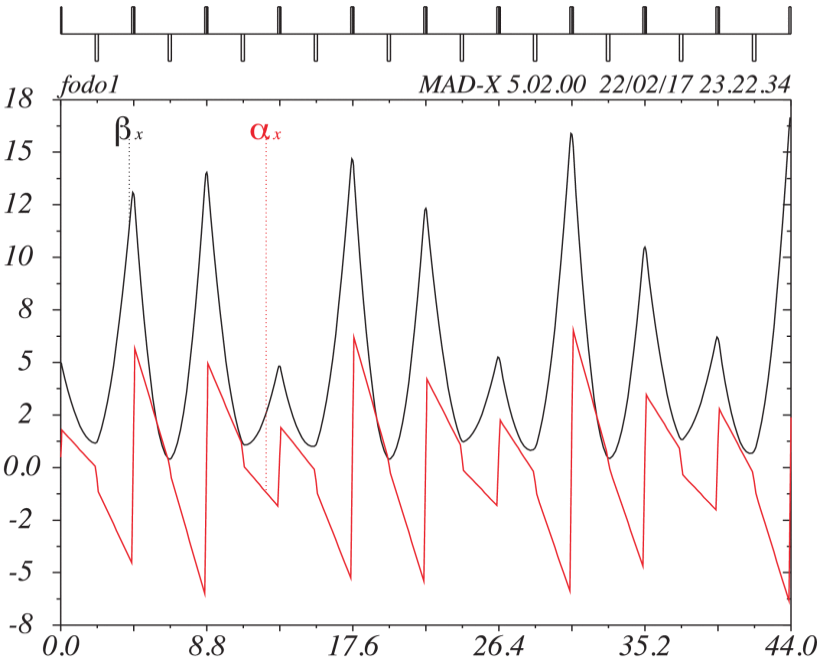
In circular accelerators, for example, in the case of possible mismatched beam injection to the ring, a periodic FODO will try to control the beam, but this will oscillate around the periodic parameters. In Figure 2 the classical Twiss description of this example does not give us any information other that the beam wiggles around the ideal fixed point with no apparent order we can find in the figure.

The same example but described using our new complex formulation as shown in Figure 3 gives us much clearer information when the different complex points are plotted after each period. The points must remain in the invariant pencil of circles that pass through the point defined by the injection parameters.

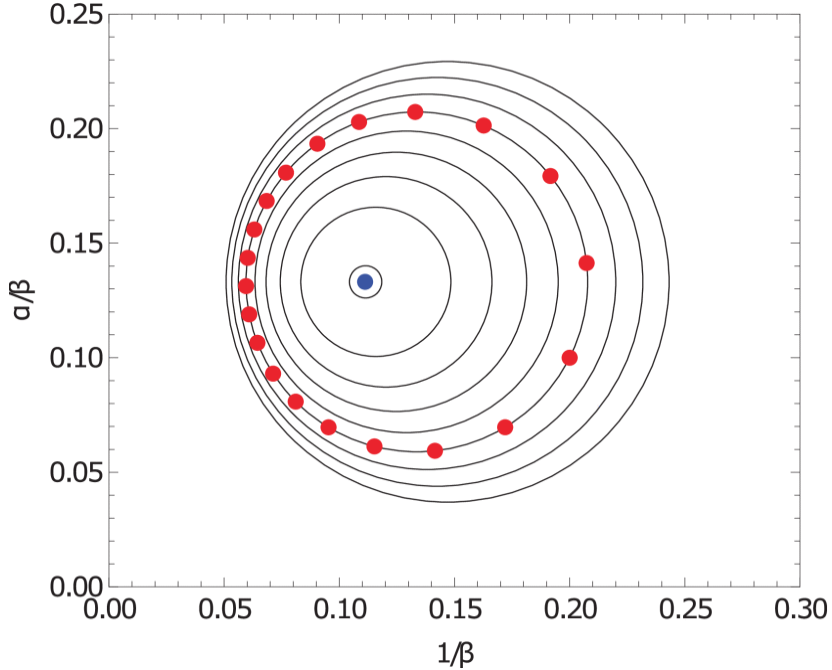
Through the newly proposed complex formulation of linear optics of particle accelerators, we have found deeper properties of beam lines. We have seen that the invariant points are nothing but invariant circles of zero radius. In this way, it is possible to obtain a higher bound of the largest beam excursion at any point.

In many ways, the presented complex formulation is equivalent to the Twiss parameters approach, but our new method generalizes and complements the classical analysis of beam transport lines. The remarkable finding that the general complex transformation of a linear beam line is a Moebius transformation allows us to prove important theorems of beam dynamics in a simpler way, and it opens the capability of transforming complete regions of the Riemann sphere instead of just single points of beam lines, as is the case in the classical formalism. The new complex formulation, apart from the elegance and compactness of the solution obtained, contributes to improve our fundamental knowledge of linear beam transport dynamics in particle accelerators and helps us in their design and construction.