Simulating particle physics in a quantum computer

Particle physics is an interesting and complicated field of study. Its theoretical framework, the Standard Model, was developed during the second half of the twentieth century and it opened he possibility to explaining the behavior of the basic blocks of the Universe. It also classified all the particles, from the electron (discovered in 1897) to the Higgs Boson (found in 2012). It is not pretentious to claim that it is one of the most successful theories in Science.
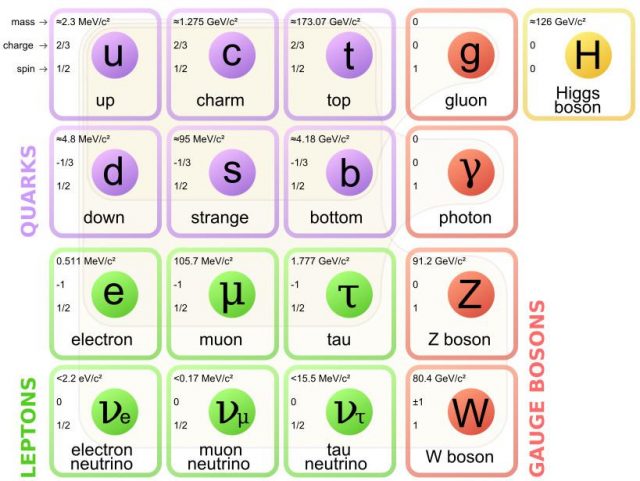
Unfortunately, the Standard Model is also a very difficult theory to handle. By using an analytic approach many problems cannot be solved and computational methods require a huge computational power. Most of the simulations about this theory are performed in supercomputers and they have severe limitations. For instance, the mass of the proton can be calculated by the use of a technique called Lattice Quantum Chromodynamics (lattice QCD), but even using a supercomputer of the Blue Gene type the error was around 2% 1. This is a huge achievement that shows the utility of the theory, but it is also a signal about the necessity of developing new numerical tools to handle this kind of calculations.
One potential solution to this problem is to use quantum systems in order to perform the simulations. This idea is at the core of the field of quantum computing and it was first proposed by one of the pioneers in the study of particle physics, Richard Feynman 2. Feynman’s idea is easy to explain. Quantum systems are very difficult to simulate by the use of ordinary classical computers but by using quantum systems we can simulate different quantum systems. If we have a quantum system that we cannot control but we can mimic its dynamics to a friendly quantum system we have solved the problem. We can just manipulate the second system and infer the results to the first one.
This idea has been recently applied to the problem of simulating particle physics problems by the groups of Peter Zoller and Reitner Blat at the Institute of Quantum Optics and Quantum Information of Innsbruck (Austria) 3. These groups have simulated the simple particle model, the Schwinger model, in one dimension. To do so they mapped the original problem to a spin model that can be simulated by using calcium ions. More specifically, they used four calcium ions confined by electromagnetic fields.
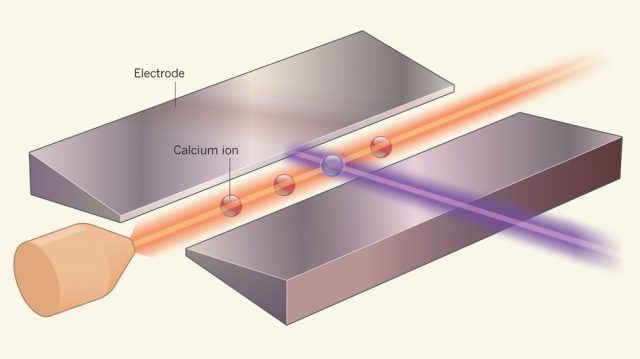
First of all, we need to clarify one thing. This simulation can be easily performed in a laptop computer. Quantum computers are not big enough yet to compete with classical supercomputers. The purpose of this study was just to perform a proof of concept.
The four ions on the experiment are controlled by laser beams. This allows the simulation of the dynamics of four lattice sites and each of them can contain a particle, an antiparticle, or just vacuum. The main purpose of the simulation was to replicate the mechanism of particle-antiparticle creation.
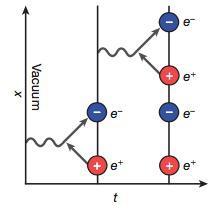
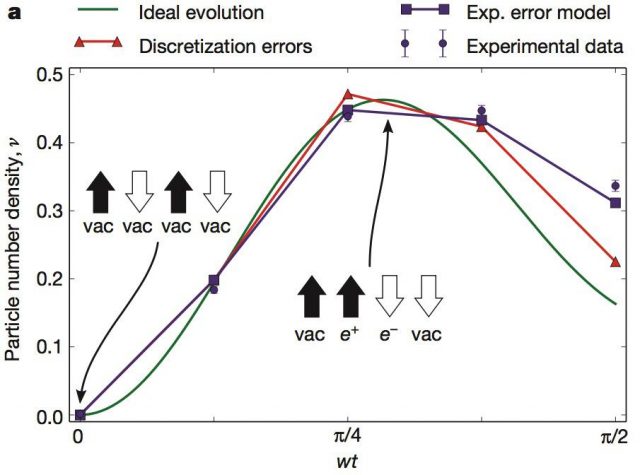
The simulation results are consistent in comparison with analytical calculations once the experimental errors were taken into account. In Figure 5, we can see a plot of the particle density as a function of time. When the simulation starts at the vacuum it evolves fast to the creation of particles and antiparticles. The errors of the experiment are very small and the results fit very weel with the theoretical predictions.
Even if this simulation can be carried in a personal computer the transcendence of this experiment is huge. It proves that particle physics can be studied by a totally different quantum system, trapped ions. As more powerful quantum computers are to come this opens the door to a totally new way of looking at the fundamental blocks of the Universe.
References
- S. Dürr et al. Ab Initio Determination of Light Hadron Masses. Science 322, 1224 (2008). ↩
- R. Feynman. Simulating Physics with Computers. International Journal of Theoretical Physics 21, 467 (1982). ↩
- E.A. Martínez et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516 (2016). doi:10.1038/nature18318 ↩
1 comment
But, could lattice gauge theories just be computed by means of regulatization/renormalization techniques? (for example, ‘lattice regularization’ makes derivatives to become finite differences).