When should a man be more interested in caring for his sister’s children than his wife’s?

From the genetic point of view, when should a man be more interested in caring for his sister’s children than his wife’s? A quantitative analysis of Alan Rogers, University of Utah, shows 1 that this behaviour should be the choice in populations where adultery is common or permitted.
In the animal world, males caring for offspring is linked to genetic relatedness: to perpetuate his genes an individual has an interest in investing on those with whom he shares his genes. Does this sociobiological hypothesis apply to humans? If so, this would mean that, in societies where infidelity is common, a man would show more interest in caring for his sister’s children, with whom he is sure to share a genetic heritage, rather than for his own wife’s children, who may be those of another man and, therefore, genetically unrelated.
The human case was first approached quantitatively in the 1970s. The models introduced at that time shared the goal of specifying conditions under which men are genetically closer to sisters’ children than to those of wives. The point at which they are equally close is called the ‘paternity threshold’.These authors assumed that selection would favour investment in sisters’ children only when paternity confidence is below this threshold. The models disagreed about its numerical value. But the lowest value —0.268— has become enshrined in the literature. But this value, which means that it is necessary that less than one out of four of a woman’s children is the offspring of his husband for him to care more for his nephews and nieces, is too low to be credible.
Furthermore, many forms of parental investment may exhibit decreasing returns to scale. In other words, the benefit from an additional unit of investment in any given offspring may decline with each unit invested. Where this is so, we might expect men to distribute investment among multiple offspring, weighting that investment in favour of those with whom they are most likely to share genes. Besides we should not forget that the optimal behaviour of males will depend in part on the responses of females. None of these complexities are taking into account in these models.
To tackle this problem, Rogers, instead of using the coefficient of relatedness, has worked with the coefficients of kinship — the probability that two genes, drawn at random from each of two relatives, are copies of the same gene in some given ancestral generation. In the absence of inbreeding, the coefficient of kinship equals half the coefficient of relatedness. Two of these coefficients are of interest, those that describe the genetic kinship of a man to the children of his wife and to those of his sister.
These coefficients depend on two probabilities, which may vary among families. The first of these— p, or paternity confidence — is the probability that a child’s father is his mother’s husband. The other is h, the probability that two siblings share the same father. The value of h is relevant because it affects the genetic relatedness of a man (Rogers calls him Ego) to his sister’s children. This value depends on paternity confidence, but not that provided by Ego’s wife. It depends instead on the paternity confidence provided by Ego’s mother to her husband. The value of h also depends on the number of a woman’s husbands. Rogers assumes that women have only one. Finally, he assumes that Ego does not know values specific to his own family and must rely instead on population averages.
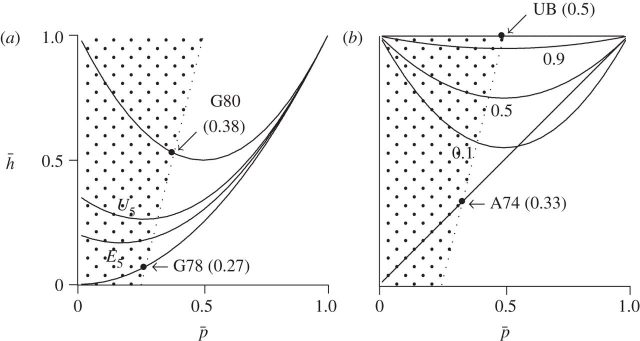
Rogers’ model shows that the models of the 1970s were based on assumptions that are too restrictive, and thus underestimate the genetic proximity of a man with his sister’s children. For example, the dominant model assumes that the probability that two children of a woman to have the same biological father, knowing that it is not the husband is zero on average. By correcting these biases and taking into account other parameters such as the number of extramarital partners a woman has, Rogers found that preferential investment in nephews and nieces may be justified if the paternity confidence p is less than 1/2, a value much more realistic.
Presumably real populations lie somewhere between these extremes. This range of uncertainty implies that there is no single paternity threshold—no single value of average paternity coefficient at which men are equally related to children of wives and of sisters. Instead, the paternity threshold varies among populations between 0.268 (the lower bound) and 0.5 (the upper). Even under the most generous conditions, the paternity threshold requires a very low confidence in paternity. In any case the sociobiological hypothesis in question appears more plausible now.
References
- A. R. Rogers, Genetic relatedness to sisters’ children has been underestimated, Proceedings of the Royal Society B, vol. 280, 1751, 2013. DOI: 10.1098/rspb.2012.1937 ↩