Pele’s hairs and the delayed breakup of viscous liquid jets

Pele is the Hawaiian goddess of volcanoes. Pele’s hairs are thin strands of molten basaltic glass drawn out from lava, thrown into the air from lava fountains, lava cascades or vigorous lava flows, and spun out by the wind. Each hair-like strand has a diameter less than 0.5 millimeters and is as long as 2 meters. Liquid jets of lava, like other highly viscous fluids, behave like a piece of rope buckling and coiling after hitting a solid surface. The formation of these long, thin liquid jets is paradoxical since the standard theory of jet breakup predicts that the growth rate of the perturbations is independent of viscosity and for inviscid fluids (like water) a jet of such diameter will breakup after a few centimeters of length. Arman Javadi (École Normale Supérieure in Paris, France) and his colleagues claim the solution of this paradox in a new paper published in Physical Review Letters ¹. The new theory explains how viscosity acts to delay jet breakup, predicting for the breakup length as a function of the flow rate and the fluid properties.

Everybody is familiar with the behavior of a jet of tap water falling into a sink. At low flow rates, drops with constant mass detach periodically at a downstream distance similar to the nozzle diameter. But as the flow rate increases, a steady jet emerges from the nozzle and breaks up further downstream. The length of the intact portion of the jet depends on in the viscosity which acts to delay jet breakup. A jet of water from a faucet with a diameter of less than one millimeter fragments after a few centimeters, whereas a thread of honey can reach up to several meters. This behavior is puzzling for the theory of jet breakup developed by the Belgian Joseph Plateau and the Englishman Lord Rayleigh in the nineteenth century.

Let me briefly review the history of the theory of jet breakup, i.e. the transition from cylinder geometry to drops ². The earliest study of the behaviour of jets and of breakup into drops was developed by Leonardo da Vinci in the Codex Leicester. Da Vinci (1508) and Mariotte (1686) claim that gravity is responsible for drop breakup, which occurs when the fluid thread becomes as “thin as a hair.” In such a case, a glass jet can extend to a length of 100 kilometers before breaking! This paradox was solved by Laplace (1805) and Young (1805) exhibiting the crucial role of the surface tension (the effect of both the axial and the radial curvature of the jet). Plateau (1843) developed a theory to explain the experiments made by Savart (1833) to confirm the role of surface tension, but a little disagreement remains, until it was finally solved by Lord Rayleigh (1879) by taking into account the role of the viscosity of the fluid. The main features of drop breakup were essentially well established after the works of Lenard (1887), Boyd (1890) and Rayleigh (1892).

The physical meaning of the surface tension γ is that of an energy per unit area, so if the surface area increases by δA, the surface energy changes by δE = γ δA. Modulations of the jet radius, like small perturbations or noise, may lower the net surface area, driving the system towards a lower energy state. This instability is caused by the fact that the Young-Laplace pressure (linearly depending on the surface curvature) increases in constricted regions, driving out the fluid and thus reducing the radius even more. Plateau and Rayleigh theory shows that all perturbations whose wavelengths are larger than the perimeter of the jet have a negative energy, thus being potentially unstable (grow in time). Starting from a random initial perturbation, the amplitudes on a jet will eventually be dominated by that with the largest growth rate, which depends on the jet dynamics. This preferred wavelength of breakup determines the drop size without introducing any length scale from the outside. Plateau and Rayleigh theory shows that the most unstable wavelength for an inviscid liquid jet is about nine times the unperturbed radius of the jet, hence a long-wavelength model describes the linear instability quiet well.

The simplest way to understand the experimental results in fluid dynamics is the use of dimensional analysis and similarity. In Ref. [1], four dimensionless parameters are used to characterize the main features of the fluid motion. The breakup length and the nozzle radius are non-dimensionalized by using the flow rate and gravity (denoted by Π_b and Π_r, resp.). The ratio of the kinetic energy of a drop issuing from the jet relative to its surface energy results in the Weber number, denoted by Π_γ. The relative effect of viscous forces and surface tension is taking into account by the dimensionless capillary number, denoted by Π_η. In order to consider the combined effect of Weber and capillary numbers, Ref. [1] also uses the Ohnesorge number, denoted by Π_Oh, which also measures the relative importance of viscosity relative to surface tension. For water, the Π_Oh number is very small, but for silicon oil, honey and lava is larger than unity.

Viscous stresses affect the dynamics of jet instabilities, but show up solely in the presence of motion since they are proportional to rates of deformation. Therefore, viscosity η does not affect the stability condition in Plateau and Rayleigh theory, although it introduces a new length scale, namely the penetration depth depending on the Ohnesorge number, analogous to the persistency length of vorticity in a viscous fluid sheared at given rate. This fact is contained in Rayleigh’s paper of 1892, in the limit of very large viscosity (Π_Oh >> 1) and by using a long-wavelength model for the disturbances. The theory predicts that the most unstable wavelengths are unaffected by viscosity, but its growth is slowed down as compared with the inviscid case. However, such slowing down of the instability when Π_Oh is large is not enough to explain observations, since it contains no explicit viscosity dependence. Such a result has been paradoxical until now.

Arman Javadi et al. [1] used an experimental setup consisting of a nozzle enclosed in a cylindrical vacuum chamber with inner diameter 19 centimeters and length 7,5 meters, with a careful system to control the flow rate such that even the longest jets (about 7,5 meters) remain perfectly straight. Silicon oils with constant surface tension, nearly constant density but a wide range of viscosities, between 50 and 27 800 cS (centistokes). The next figure shows the breakup length as a function of flow rate for three different viscosities; as expected, it is an increasing function of both the flow rate and the viscosity.

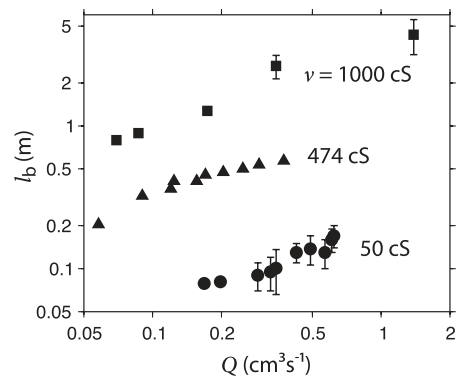
The analysis of the experimental results obtained by Arman Javadi et al. shows that the values of the dimensionless parameters of the fluid change during the growth of the perturbation before the jet breakup. The authors develop a new theory based on the local validity of that of Plateau and Rayleigh, but considering a change of the Ohnesorge number as function of the axial distance; in fact, the experimental results show that Π_Oh number changes between 0.65 and 2160 for very long jets. The new theory shows that there are two different regimes depending on Π_Oh number, a viscosity-independent limit for Π_Oh <<1, and a (less familiar) viscosity-dominated limit for Π_Oh >>1; which limit is relevant depends on the position along the jet, slowing down of the instability and changing the jet radius for breakup estimated by using a constant Π_Oh.

In my opinion, the answer to the paradox has been a real surprise for those working in the field, since a “truly new” theory has not been required, only a clever reinterpretation of the dimensionless parameters of the standard one; locally, Plateau and Rayleigh theory remains valid (although the estimation of the breakup length using constant dimensionless parameters has been a very bad approximation for highly viscous liquids during the last century). As usual in physical sciences, the solution is based on the results obtained by carefully designed and executed experiments. The unexpected large change in the Ohnesorge number along the jet length explains without surprise that the viscosity has a strong influence on the observed breakup lengths.

Arman Javadi et al. do not consider in their paper the formation of Pele’s hair, but their results can also be used to explain the formation of these glass fibers from molten rock. The fast cooling of the lava jets results in a strong increase in viscosity, so the threads are stretched very thin without breakup before their solidification and subsequent breakup. Obviously, further experimental studies are required for a complete understanding of the dynamics behind physical phenomenon as curious as Pele’s hair.