C2 molecule, doubly or quadruply bonded?

One of the multiple tasks of quantum chemistry is the rationalization of the bonding between atoms to form molecules. In this vein, two main aspects are clearly distinguished: i) the binding energy, or the energy gained by the molecule when two atoms are bonded; and ii) the bond order (how many bonds are the responsible for such binding). One may think that both are connected, but this is not always so, and, in the case of C₂, there is a vivid debate within the chemical community regarding it’s bond order. While some calculations, based on Valence Bond (VB) theory predict a bond order of four ¹ (quadruple bond) others, based on Molecular Orbital (MO) theory, predict a bond order of two (double bond). Apparently, these two results are contradictory. Nevertheless, we have to keep in mind that both methods are approximate. In a recent publication ², we have approached the problem using a different method, the Natural Orbital Functional theory (NOFT). Our results predict a quadruple bond for this molecule, in agreement with recent VB calculations. In addition, they provide a connection with the apparently contradictory MO results. Let us get into the details of the chemical bond of this intriguing molecule.

Binding energy, in diatomic molecules, is calculated as the energy difference between two geometries: the equilibrium geometry and the “infinitely” separated atoms (see Figure 1). This value can be measured experimentally, and theoretical predictions must agree with the experimental value. Therefore, from the theoretical perspective, in order to calculate accurately the binding energy, we have to calculate accurately both the total energies at these two points. This is not an easy task. In fact, the exact total energies cannot be calculated for molecules with more than one electron, like H₂⁺. For molecules with more electrons, the exact solution is unaffordable in general, and approximate methods must be used. Earlier developed VB and MO methods where based on the model of each electron occupying an orbital. The shape of the orbitals used in these approaches is one of the main difference between VB and MO. While VB theory allows for atomic orbital hybridization (leading to the known sp, sp², sp³ hybridizations), MO theory assumes that no hybridization occurs at atomic level. Obviously, the shape of the molecular orbitals resulting from the overlap of these orbitals is different. We will come to this point later. With these “simple” models, one calculates roughly 99% of the total energy of a molecule. One may think that this is an astonishing achievement. However, the remaining 1% (called correlation energy, due to electron-correlation effects) is crucial in calculating binding energies within chemical accuracy. When electron correlation effects are included, the “one-electron” in “one-orbital” picture is lost. The price paid to be able to calculate accurately binding energies is that we end up with orbitals with occupation numbers different from 1 (occupied) or 0 (unoccupied). These new orbitals are called Natural Orbitals. The occupation numbers are now allowed to be, for instance, 0.9. This does not mean that electrons are broken (we cannot find 0.9 electrons) but that the probability of finding an electron in that orbital is 90%.

Both in VB and MO approaches there are high-level methods that take into account electron-correlation, but natural orbitals are considered implicitly. The shape of the orbitals used throughout these calculations are “imposed” a-priori. NOFT was developed somewhat later, and in this approach the total energy of the molecule is calculated explicitly in terms of the natural orbitals and their occupation numbers. Once electron correlation is included, calculated total energies may reach to 99.99-100% of total energies, and, therefore, the calculated energy differences lie within chemical accuracy. Having this in mind, let us focus now on the different pictures yielded by these approaches to the binding in C₂ molecule, having in mind that they all provide accurate binding energies.

MO and VB picture

Molecular orbitals are formed combining similar atomic orbitals. In the MO approach, each carbon atom has four valence orbitals, namely, a 2s and three 2p. These 8 atomic orbitals lead to 8 molecular orbitals (the lowest-lying 5 orbitals, with their occupations, in Figure 2). The formal bond order calculated with these orbitals and occupation numbers is 2 (resulting from 6 electrons in bonding orbitals and 2 in an antibonding orbital).

In VB, the bond picture arises from considering that the C atom bears a sp hybridization. In the resulting bond picture (see Figure 3) 6 electrons are clearly in bonding orbitals. The remaining two are claimed to form a weaker bond (the forth bond), although apparently they do not form any formal bonding orbital. Based on these high-level calculations, authors were able to estimate the strength of this weak bond. It resulted to be indeed very weak.

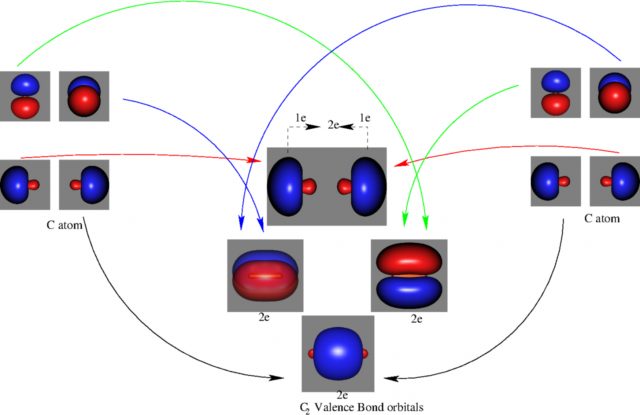
However, we have to recall again that orbitals and orbital energies are not measurable experimentally. Based on this, other authors believe that these conclusions are incorrect. In fact, some authors claim that the orbitals from MO picture are the only ones to have a physical meaning, as it was demonstrated by Koopmans. Koopmans’ theorem connects the ionization energy of a molecule with the negative of the energy of the highest occupied molecular orbital (HOMO). Nevertheless, when electron correlation is taken into account, orbitals calculated by MO theory do not have associated energies. Therefore, the choice of the orbitals remains arbitrary.

NOFT picture

The approach developed by M. Piris et. al. in our group (PNOF5), considers explicitly the natural orbitals and occupation numbers to calculate the total energy. No a-priori assumption of the orbitals’ form is made. The obtained orbitals and occupation numbers are those that minimize the energy expresion. As MO and VB theory with correlation effects included, no energies can be associated to each of the orbitals. In this way, the Natural Orbital representation is obtained, with orbitals and occupation numbers.

Based on the obtained results, we observe sp³ hybridization for each carbon atom, leading to four bonding and four antibonding orbitals. The 8 electrons mainly occupy the bonding orbitals, therefore leading to a formal bond order of four, as VB calculations predicted. In addition, it is possible to obtain orbital energy values performing some further mathematical operations, but then orbitals are changed. Associated to these energies orbitals similar to those of MO theory are obtained. The prize paid is that no orbital occupation numbers are now available. These orbital energies are closely connected with the ionization potential of the molecule, namely, the physical process of removing electrons from the molecule. In order to calculate bond orders, orbitals and occupation numbers are needed, and therefore the Natural Orbital picture must be considered, and therefore, we conclude that the bond order in C₂ is four, a quadruple bond.

Both NO and CO pictures agree well with VB and MO pictures, but, for calculating bond orders, we think that MO approach is not flexible enough regarding the shape of the orbitals, leading to an incorrect bond order. Nevertheless, we have to keep in mind that PNOF5 is also an approximate method. C₂ is a particularly challenging case (for most other molecules all methods agree) and the last word regarding this issue is yet not said.

About the author: Jon M. Matxain obtained his Ph.D degree at the University of the Basque Country, in the field of Theoretical Chemistry, applied to the optical properties of semiconducting nanoclusters. He moved to Sweden, where he focused on the field of theoretical biophysics. Now, he is a Ramón y Cajal Fellow at the University of the Basque Country. His main interests are nanomaterials, radical oxidation of proteins, and the applications of the Natural Orbital Functional Theory.