The sky is blue, clouds are white, and the transmission of light through dense media

Newton suggested that the apparent colours of natural objects depend on which colour is most strongly reflected or scattered to the viewer by the object. In general, there is no simple way of predicting from the surface structure, chemical composition, etc., what colours a substance will reflect or scatter. However, the blue colour of the clear sky can be explained by a fairly simple argument.

As Thomas Young showed experimentally, different wavelengths of light correspond to different colours. The wavelength of light may be specified in units of nanometres. The range of the spectrum visible to humans is from about 400 nm for violet light to about 700 nm for red light. Small obstacles can scatter the energy of an incident wave of any sort in all directions, and the amount of scattering depends on the wavelength.

This fact can be demonstrated by simple experiments with water waves in a ripple tank. As a general rule, the larger the wavelength is compared to the size of the obstacle, the less the wave is scattered by the obstacle. For particles smaller than one wavelength, the amount of scattering of light varies inversely with the fourth power of the wavelength. For example, the wavelength of red light is about twice the wavelength of blue light. Therefore, the scattering of red light is only about one-sixteenth as much as the scattering of blue light.

Now it is clear why the sky is blue. Light from the sun is scattered by separate molecules of vapour, particles of dust, etc., in the air above, all of which are usually very small compared to the wavelengths of visible light. Thus, on a clear daylight of short wavelengths (blue light) is much more strongly scattered by the particles than is the light of longer wavelengths, and so-to-speak fills the firmament from end to end. When you look up into a clear sky, it is mainly this scattered light that enters your eyes. The range of scattered short wavelengths (and the colour sensitivity of the human eye) leads to the sensation of blue. On the other hand, suppose you look at a sunset on a hazy day. You receive directly from the Sun a beam that has had the blue light almost completely scattered out in all directions while the longer wavelengths have not been scattered out. So you perceive the Sun as reddish.

If the Earth had no atmosphere, the sky would appear black, and stars would be visible by day. In fact, starting at altitudes of about 16 km, where the atmosphere becomes quite thin, the sky does look black, and stars can be seen during the day, as astronauts have found.

If light is scattered by particles considerably larger than one wavelength (such as water droplets in a cloud), there is not much difference in the scattering of different wavelengths. So we receive the mixture we perceive as white.

But what happens when the medium through which the light is propagating is quite dense? In this kind of media different characteristics of the light waves change continuously because of the interaction with particles that are very close to one another: phase, amplitude and wavelength change randomly in time and space. Thus, it seems quite difficult to describe what may occur in this conditions and explain the increase in total transmission that is actually measured contrary to what would be expected.

Now a group of researchers, including Juan José Sáenz, an Ikerbasque Research Professor at DIPC, has developed a new propagation model¹ that takes account of what happens very close to the particles (near-field) and explains the paradox of the increase in transmission. They have tested it using computer simulations and experimentally.

In a dense medium, in the direction of propagation, as light is scattered by every particle, one may expect that in a large enough distance not much of the original light, the so-called specific intensity, will remain. Actually, we could expect that, for a given distance, the denser the medium the smaller the specific density remaining. But this is not what is measured experimentally.

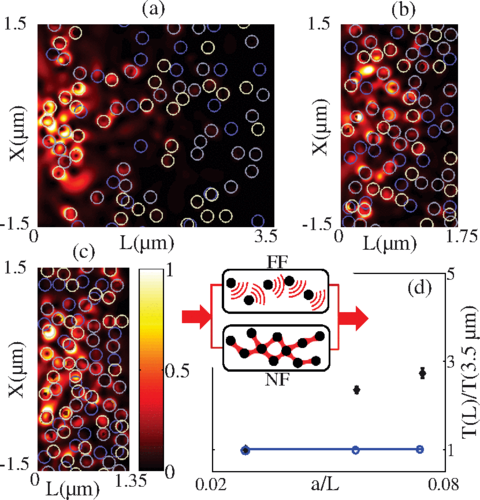
There are some effects to be taken into account: for example, if separation between scattering centres is much larger than the wavelength, the scattering events are considered to be independent, implying that only the size of the particles and how packed they are will influence the transport of light. But if the separation is smaller the scattering events are not independent anymore, and we may find interferences. These interferences may imply that some of the dispersed energy is back to the line of propagation with a certain probability, thus increasing the transmission.

When propagating in highly scattering media, then, the energy is not only carried by propagating waves but it also evolves through evanescent coupling between individual scatterers. For linear random media, as scatterers become optically connected, the near-field coupling between particles can be seen as an opening of new transmission, optically connected, channels.

The researchers show that a new regime of transmission emerges, which can be described in terms of physically meaningful and measurable quantities such a near-field scattering cross section. This near-field corrected transport not only improves the macroscopic description of light propagation in random media but it also enhances the predictive capabilities of light transport models.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.