Einstein and quantum solids
One of the first recognized successes of the early quantum theory arose, not from the study of radiation, but from the theory of solids. Once again in the physics of the first half of the 20th century Albert Einstein was at the forefront; but this time the story is seldom told.
After presenting the hypothesis of light quanta in 1905, which explained the photoelectric effect, Einstein showed in 1906 that Planck’s earlier results on the distribution of energy in electromagnetic radiation could be derived using two assumptions.
The first, already familiar from his 1905 work, was that light is composed of light quanta; the second was that the light quanta are emitted and absorbed by oscillating charges within matter that are vibrating only with certain quantized energies. This means that light is emitted by oscillating charges within matter, as might be expected from Maxwell’s theory, but the energies both of the emitted light and of the oscillators are restricted to certain quantized values, which contradicted classical theory. The oscillators behaved like charges attached to springs, oscillating back and forth with certain frequencies corresponding to certain allowed quantum energies.
In 1904, the German physicist Paul Drude had proposed a model of a crystalline solid in which the atoms are arranged in a lattice such that each atom is bound to its neighboring atoms by bonds that can act like little oscillator springs. Drude showed, using classical physics, that the three dimensional oscillation of the lattice atoms can account for the observed absorption of infrared radiation by some solids, if the atoms are assumed to be ionized. A similar oscillation of the electrons, attached to the atoms or ions, accounted for the observed absorption of ultraviolet radiation in solids.
In 1907 Einstein applied the quantum hypothesis to Drude’s classical oscillators. Even before Drude’s model, Einstein had been wondering as early as 1901 whether the internal kinetic energy of solids and liquids might be regarded as the energy of “electric resonators.” One outstanding puzzle at that time involved the behavior of the specific heat, c, of solids as the temperature decreased. Normally the specific heat is assumed to be constant in the relationship between the transfer of heat, ΔQ, and the change in temperature, ΔT, of a mass, m,
ΔQ = mc ΔT
Applying classical physics to Drude’s oscillator model of the atoms in a lattice confirmed that the specific heat C should be a constant for solids at all temperatures. However, when Einstein applied the quantum hypothesis to the oscillators in Drude’s model, he obtained an expression for the specific heat indicating that the value of the specific heat should change with temperature. While remaining constant at room temperature and slightly below, the specific heat would drop precipitously to zero at the temperature declined to zero. Conversely, as the temperature increased from 0 K, Einstein’s value for the specific heat of a crystalline substance as a function of its temperature should approach the constant value at room temperature.
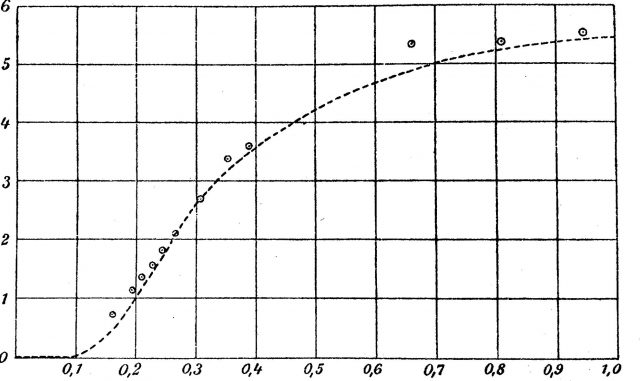
Einstein’s predictions for the behavior of the specific heat of solids as a function of temperature were based on an application of the quantum hypothesis to a model of a crystalline solid in which the lattice atoms behave as three-dimensional oscillators vibrating with quantized energies.
The physicists Walther Nernst and Frederick A. Lindemann, working in a low temperature laboratory in Berlin, astonished their colleagues with a complete confirmation of Einstein’s prediction for the way the specific heat of a crystalline solid changed with temperature. It was the first confirmation of the quantum hypothesis outside of the field of radiation, and it clearly indicated that crystalline solids could be treated as an array of oscillating lattice atoms subject to requirements of quantum theory and, later, quantum mechanics. This model has served as the basic model of a crystalline solid ever since. DIPC’s researchers actually work using improved versions of it.
References:
Asimov, I. (1993) New Guide To Science Penguin Press Science
Cassidy, D. et al (2002) Understanding Physics Springer Verlag New York
Pais, A. (1979) Einstein and Quantum Theory Reviews of Modern Physics 51 – 4
Author: César Tomé López is a science writer and the editor of Mapping Ignorance.
5 comments
[…] A Einstein se le recuerda por muchas cosas; pero se menciona poco que fue él quien demostró que la cuántica también gobernaba el comportamiento de los sólidos en 1907. En el canal DIPC, Einstein and quantum solids. […]
[…] Posted in Noticias, Science, Condensed matter, DIPC, Physics | 0 comments […]
[…] Einstein and quantum solids […]
[…] Picture credit. […]
[…] [1] Este artículo es una adaptación de nuestro Einstein and quantum solids […]