Why do some materials conduct electricity and others don’t? (2): The band theory of solids

Condensed matter • DIPC • Physics • Science

By DIPC January 14, 2016 1 comment Print

In 1928, just two years after the formulation of quantum mechanics, the German physicist Arnold Sommerfeld modified the classical free-electron model by treating the electrons according to quantum mechanics. But the new theory still contained the unrealistic assumption that the electrons do not interact with the charged lattice ions except to collide with them. As before, Sommerfeld also considered the electrons to be little charged particles of matter.

The electron is formed from standing waves of energy. | Credit: Mauritsson et al (2008) Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope, Phys. Rev. Lett. 100, 073003

Beginning in the same year, Felix Bloch, an assistant to Werner Heisenberg in Leipzig, began to make more realistic assumptions in an attempt to formulate a more complete quantum mechanics of electrical conductivity. First, because he wanted to assign a definite momentum and energy to each of the electrons, but not a definite position or a time interval, he chose the wave side of the wave-particle duality. He assumed that the electrons behave, not like particles, but like infinitely extended de Broglie waves. As a result, Bloch did not treat electrons inside metals as a “gas” of particles, but rather as periodic waves extending throughout the periodic crystal lattice. This, it later turned out, helped to explain how electricity can begin to flow in a wire the instant a wire is plugged into a wall socket. If the electrons are viewed as balls of matter, it would take a small amount of time for the current to begin flowing at the rate specified by Ohm’s law.

Bloch made a second assumption. He assumed that the positive metal ions, which are arranged in an infinite, periodic array (that is, in a perfect crystal), each exerts an attractive electric force on the negative electrons. This attractive force formed in visual terms a potential energy that looked like a type of “potential well.” The wells of neighbouring ions then overlapped so that together they formed a periodic arrangement that gave the electron waves a very bumpy ride down the wire.

Bloch then solved the Schrödinger equation for the energies that these types of de Broglie waves (wave functions) could possess while moving in this type of periodic potential. He discovered that the allowed energies of the electrons in the material are joined together into bands of quantum states, just as there are certain quantum stationary states within each atom in which the electrons are allowed to exist. Between the bands, as between the quantum states, there is a range of energies in which electrons are forbidden to exist. The bands in the material are actually created by the joining together of the quantum states of the individual atoms. In fact, if there are a total of N identical atoms in the material, then there are N quantum states within each band. According to a rule in quantum mechanics (the Pauli exclusion principle), only two electrons are allowed to occupy any one quantum energy state of a single atom, and this is allowed only because the two electrons spin on their axes in opposite directions.

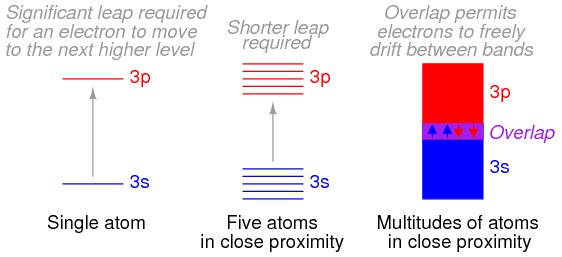
As extended and refined by Bloch and others during the 1930s, Bloch’s theory, known as the band theory of solids, accounts very well for the conducting behaviour of materials. When atoms are joined together into a crystal, each of the individual quantum states of the atoms joins with the corresponding states in other (identical) atoms in the crystal to form the various energy bands within the material. The electrons in the atoms then fill up the available states within each band. For instance, if there are N atoms in a material, there are N states in a single band and up to 2N electrons in each band (since two electrons can occupy one energy state if they spin in opposite directions).

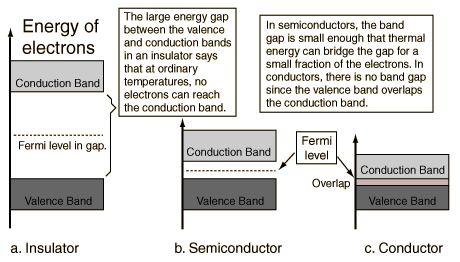
Credit: HyperPhysics — Credit: Nave (2012)

The interesting physics occurs at the top of the filled bands. When an external electric field (voltage) is applied to the material, an electron can respond to the field only if it can move up to a slightly higher quantum state, since it would have slightly more energy in responding to the field. This is possible only if there are some nearby free states to which the electron can jump. This is the case for conducting metals, such as copper and silver, since as their electrons fill in the available states, the highest band is only partially filled. The electrons in this band, which is called the conduction band, are then free to be conducted (actually, propagated as waves) down the wire, since there are empty quantum states nearby in their energy band. But the electrons in the filled lower bands are not able to move, since there are no free states nearby.

On the other hand, if the filling of the states within the bands stops exactly at the top of a band, then the electrons cannot respond normally to an electric field by moving down the wire, since there is an energy gap preventing them from reaching a quantum state in which they can move freely. Such a material would then be an insulator. An example is diamond, in which the highest filled quantum state also fills out an energy band. This band is called the valence band, since it is occupied by the outer valence electrons of the atoms. The energy gap to the next band, which is empty, is about 6 eV, so the electrons in diamond cannot normally reach the conduction band and diamond is therefore a good insulator.