System of quadrotors for the transportation of deformable linear objects

Nowadays, the industry is centering their efforts on the development of single aerial robots carrying single objects, such as the widely-known drone of Amazon for delivering packages, which was followed by some national post-office services. However, other approaches go a step further and get to transport bigger objects in a cooperative way, reducing the payload of each drone and thus, increasing their battery duration. Besides, this cooperative transport might not only be used for retail services and packet deliveries, but for another completely different type of services and tasks.
Two recent examples of these approaches appear in 1 and 2. The approach in [2], in which this article will focus and is represented in Figure 1, proposes a basic strategy for deformable linear objects (DLOs) transportation. A wire, rope, or hose can be modelled as a physical DLO.
The study here is restricted to the quasistationary state when the drones are at cruise height and the DLO is freely hanging at full length. Then, the hose can be modeled as a catenary curve, or a collection of catenary curves sharing extreme points, and its transportation can be modeled by transformations between catenary curves. The catenary is the ideal hyperbolic shape of a DLO whose unique load is its own weight, and it is an example of a funicular rigid solid of classic Applied Mechanics. It is the model of a perfect 1D rigid solid at equilibrium, corresponding to a quasi-stationary state of a DLO. A long hose divided into two sections, is transported by three drones (n = 3), so that always n quadrotor UAVs carry a hose of n−1 sections, as represented in Figure 1.
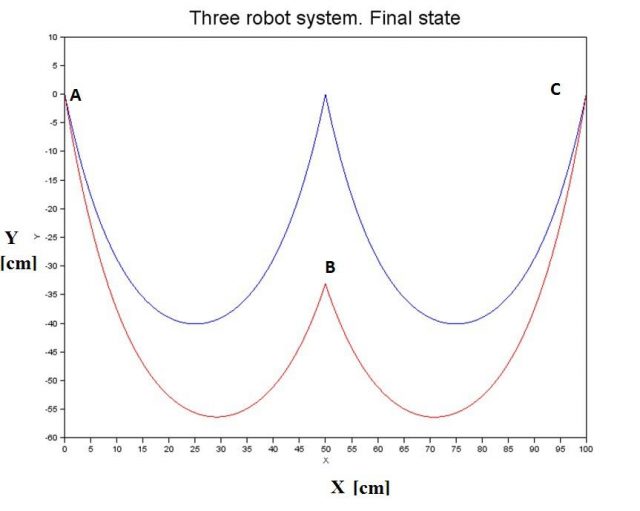
For practical reasons, we aim to have identical vertical forces exerted by the hose on all quadrotors, so that energy expenditure is the same for all, which assures that the autonomous lifespan of equivalent drone models carrying the task will be almost the same. In the case of a three drones system, this strategy implies that the quadrotor in the middle must descend in order to achieve the equal vertical load distribution. This descent will depend on the horizontal distance among drones, the length of the catenary trams and its load. An example of this desired balance state is shown in the two catenary spans in Figure 2, where node B descends the required distance while A and C nodes keep height.
However, the vertical balance process is not the final aim of this approach, but the DLO transportation in space. Thus, it represents a challenging task where drones kinematics are constrained by two factors:
-
Drones relative horizontal distance among them must preserve some limits in order to get the catenary shape DLOs.
-
Drones need to keep the desired vertical equilibrium and re-adapt their height position if necessary depending on the horizontal distances among them.
This purpose requires a very precise and careful control implementation, and it is highly encouraged that the resultant control circuits easily adapted to the transportation system different conditions: catenary weight and distance, drone dynamic parameters, displacement speed or even external perturbations.
Due to all these restrictions, adaptive online control turns to be one of the most suitable strategies to meet the objectives in this approach.
References
- Koushil Sreenath and Vijay Kumar (2013). Dynamics, control and planning for cooperative manipulation of payloads suspended by cables from multiple quadrotor robots. Robotics: Science and Systems (RSS) ↩
- Julián Estévez, Jose Manuel Lopez-Guede, Manuel Graña (2015). Quasi-stationary state transportation of a hose with quadrotors. Robotics and Autonomous Systems, 63 (2), pp 187-194. DOI 10.1016/j.robot.2014.09.004 ↩
2 comments
[…] que han realizado dentro del grupo de la UPV/EHU en torno a los drones. También han trabajado en la investigación de un sistema de transporte colaborativo entre drones con objetos lineales deformables, como cables, cuerdas o mangueras; y recientemente […]
I have a question about this, If the hose modelled as a catenary has little more mass on the bottom catenary sag or has a tap etc. Does it become a flattened catenary or semi flatenned catenary