What does the “we don’t understand how artificial intelligence takes decisions” statement mean?

Specialized media sometimes publishes similar headlines to the title of the present article. For instance 1, 2, 3, 4, 5 or 6. They are all referred to deep learning, which is a part of artificial intelligence. However, if we get algorithms to work and achieve advanced intelligent applications, what is exactly not understandable?

Deep learning is based on neural networks, which is just a way of artificial learning. An example of a neural network with a single hidden layer is shown in next figure, where x and y represent input and output values, respectively. w and b are used for the weight and the bias:

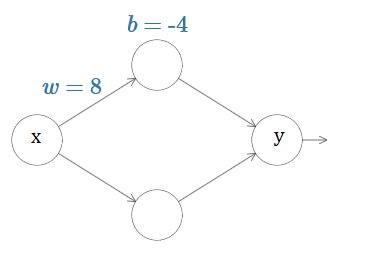
what’s being computed by the hidden neuron is: , where is the sigmoid function. Neural networks are trained so that inputs obtain specific outputs, and this is what scientists and programmers pursue. However, the output of the system is quite sensible to bias and weight, as can be seen in the following video:

Now it comes the shocking part, named as the universal approximation theorem. This rule assures that a feed-forward network with a single hidden layer containing a finite number of neurons can approximate any continuous function, under mild assumptions on the activation function. In 1989 it was proved that this theorem was true for the sigmoid activation function. In other words, the simple neural network shown before can approximate any continuous function. The bigger the number of nodes of the hidden layer, the better the approximation of the function

Now, substitute y for f(x) in the image before. x, w, and b can be tuned so that they approximate to any continuous function, and this is exactly what scientists don’t understand well. They get the output-input relations and understand the mathematics, but they can’t predict how the mapping and evolution of the tuning of the neural network will be due to the infinite number of possibilities. Neural networks can approximate to any function that you can imagine. For instance, given a function it is sure that it exists at least one neural network whose output is that function.

Deep learning makes reference to neural networks of many hidden layers, where many degrees of freedom and parameters to tune exist. It is a very used technique for complex AI problems today, and universal approximation theorem can be applied also to know why scientists don’t understand exactly how neural networks learn. This fact could lead to undesirable results or not planned learning.

References

[1] Guoqiang Zhang, B. Eddy Patuwo, Michael Y. Hu, Forecasting with artificial neural networks:, International Journal of Forecasting, Volume 14 (1), 1998, Pages 35-62, ISSN 0169-2070, doi: 10.1016/S0169-2070(97)00044-7.

[2] Michael A. Nielsen, “Neural Networks and Deep Learning“, Determination Press, 2015