Introducing a new global method to calculate electron correlations

Electrons do not move around nuclei in defined curved orbits. Our current understanding of how electrons are to be found in atoms and molecules is based on clouds of probability called orbitals as it is not possible to give a definite path for an electron.

Thus, an orbital is a region in which an electron (only one) may be found in an atom or molecule. According to wave mechanics, the electron has a certain probability of being in a given element of space. The probabilities of finding an electron in different regions can be obtained by solving the Schrödinger wave equation to give the wave function, ψ, and the probability of location per unit volumen is |ψ|². Hence, the idea of electrons in fixed orbits has been replaced by that of a probability distribution around the nucleus. Orbitals are then represented by surfaces enclosing the space in which the electron is likely to be found with high probability.

In molecules the valence electrons move under the influence of at least two nuclei (in a bond involving two atoms). Therefore, a molecular orbital is one-electron wavefunction describing an electron moving in the effective field provided by the nuclei and all other electrons of a molecular entity of more than one atom. It is convenient to consider molecular orbitals as the overlap of atomic orbitals.

But the solution of the quantum mechanical many-electron problem is one of the central problems of physics and far from trivial. A great number of schemes that approximate the intractable many-electron Schrödinger equation have been devised to attack this problem for a given molecule. As P.A.M. Dirac put it:

The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be solvable.

Probably the most popular method at present is density functional theory (DFT) . DFT is based on the Hohenberg-Kohn theorem which asserts that the electronic charge density completely determines a many-electron system and that, in particular, the total energy is a functional of the charge density. In other words, it considers a electron density in the molecule, as if the system behaves exactly as if the electrons were spread out into a continuously distributed charge, instead of the wave functions of individual atoms. Attempts to construct such a functional for the total energy have not been very successful because of the strong nonlocality of the dynamic term.

Now, Mario Piris, an Ikerbasque research professor working at DIPC and UPV/EHU, proposes ¹ a global method to calculate electron correlations from a different perspective based on so-called natural orbitals. Natural orbitals are defined as eigenfunctions of the spinless reduced electron density matrix, a matrix that appears when you treat the system and its electron wave functions in linear-algebraic terms, in what is known as Hartree-Fock aproximation.

Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons. In electronic structure theory, accurate solutions require a balanced treatment of both static (nondynamic) and dynamic correlations. Static correlation generally implies a limited number of nearby delocalized orbitals with significant fractional occupations. Conversely, dynamic correlation involves a large number of orbitals and configurations, each with a small weight.

Single reference correlation methods are well-established for the dynamic correlation, but are unsatisfactory for systems with static correlation. Piris proposes a single-reference method capable of achieving both dynamic and static correlations even for those systems with significant different possible configurations.

In this approach, a natural orbital functional (NOF) is firstly used for capturing all static correlation effects. Then, the total energy is approximated as the sum of the Hartree-Fock energy obtained with corresponding natural orbitals; plus the dynamic energy correction, derived from a properly modified second-order Møller-Plesset perturbation theory (MP2); and the nondynamic correction, obtained from the pure static component of the new NOF.

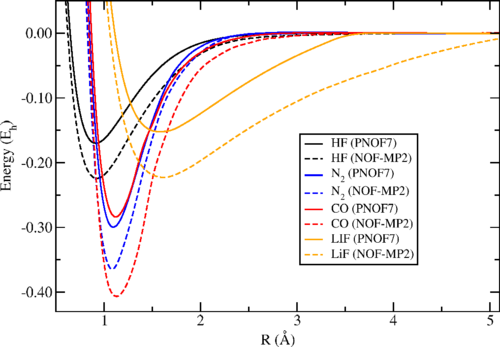
Piris applies the new procedure, that he calles NOF-MP2, to the homolytic dissociation of a selected set of diatomic molecules, paradigmatic cases of near-degeneracy effects, with the values obtained in good agreement with the experimental data.

The resulting working formulas obtained allow for static and dynamic correlations to be achieved in one shot. With efficient approaches, based on recent developments of NOF and MP2 theories, the NOF-MP2 method could become a valuable tool for treating large systems with hundreds of atoms.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.