Higher-order topological insulators

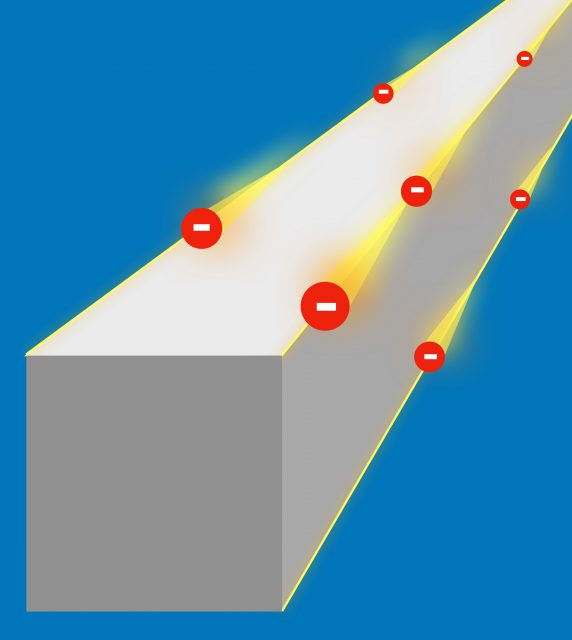
Topological insulators are materials with special universal properties, which are protected against perturbations. Such properties are theoretically described by topology, a branch of mathematics concerned with the properties of geometrical objects that are unchanged by continuous deformations. Concretely, topological insulators are electronic materials that have a bulk band gap like an ordinary insulator but have conducting states on their boundaries, i.e., edges or surfaces. The conducting surface is not what makes topological insulators unique, but the fact that this surface state is particularly robust, potentially due to some symmetry like time-reversal.

Thus, in general, we can say that a topological insulator of d dimensions with a given symmetry is insulating in the bulk but supports gapless boundary excitations that cannot be removed by local boundary perturbations without breaking the symmetry. In 2017 Benalcazar et al published in Science ¹a generalization of this bulk-boundary correspondence. In two and three dimensions, these insulators exhibit no edge or surface states, respectively, but feature gapless, topological corner excitations corresponding to quantized higher electric multipole moments.

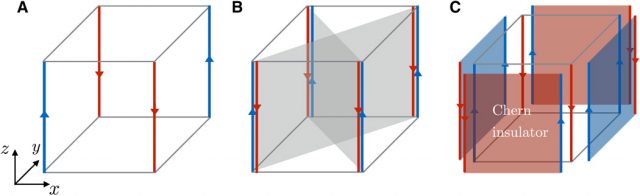
Now, a team of researchers, including Maia G. Vergniory (DIPC, Ikerbasque, UPV/EHU) & Andrei Bernevig (Princeton University), introduce ² a new class of three-dimensional topological phases to which the usual form of the bulk-boundary correspondence also does not apply. The topology of the bulk protects gapless states on the hinges of the three-dimensional crystal, while the surfaces are gapped. Both systems, with gapless corner and hinge states, respectively, can be subsumed under the notion of higher-order topological insulators (HOTIs): An n^th-order topological insulator, then, has protected gapless modes at a boundary of the system of codimension n. It follows that what they present is a second-order three-dimensional topological insulator, while the study of Benalcazar et al. introduced second-order topological insulators and third-order three-dimensional topological insulators.

The important aspect of three-dimensional HOTIs is that they exhibit protected hinge states with (spectral) flow between the valence and conduction bands, whereas the corner states have no spectral flow. The topological properties of HOTIs are protected by symmetries that involve spatial transformations, possibly augmented by time reversal. The researchers propose two cases: (i) Chiral higher-order topological insulators protected by the combination of time-reversal and a fourfold rotation symmetry. (ii) Helical higher-order topological insulators protected by time-reversal and mirror symmetries.

Therefore, the predicted new class of topological insulators show most interesting conducting properties. The current of topological electrons cannot be stopped by disorder or impurities. If an imperfection gets in the way of the current, it simply flows around the impurity. Moreover, if the crystal breaks, the new edges automatically also conduct current.

But, where to find these new higher-order topological insulators? The time-reversal symmetry breaking topological insulators akin to those of the integer quantum Hall effect may be realized in magnetically ordered crystals; and the researchers propose the naturally occurring rhombohedral or a uniaxially distorted phase of SnTe as a material realization for a time-reversal symmetric system.

Author’s note: Comments and suggestions by Maia G. Vergniory and Titus Neupert to the original version of this article are much appreciated.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.