3D topological photonic crystals whith Chern vectors at will

Some materials have special universal properties protected against perturbations. Such properties are theoretically described by topology, a branch of mathematics concerned with the properties of geometrical objects that are unchanged by continuous deformations. So-called topological insulators are electronic materials that have a bulk band gap like an ordinary insulator but have conducting states on their boundaries, i.e., edges or surfaces. The conducting surface is not what makes topological insulators unique, but the fact that it is protected due to the combination of spin-orbit interactions and time-reversal symmetry.

A topological invariant is a geometrical quantity that remains unchanged by continuous deformations. Topological invariants have found widespread applications in physics, chemistry, and materials science. One of the best known topological invariants in condensed matter physics is the Chern number.

The definition of the Chern number is not exactly simple. But it could be enough to understand the Chern number as an integer that characterizes the topology of filled bands in two-dimensional lattice systems. A band with a non-zero Chern number is topologically non-trivial. When the highest occupied band is non-trivial and completely filled, the state is called a topological insulator. A material whose topological phases can be characterized by the Chern number is called a Chern insulator, a class of topological insulators.

But when we make Chern insulators interact with light, something interesting happens. Electrons are spin-1/2 particles, whereas photons are spin-1 particles. The distinct spin difference between these two kinds of particles means that their corresponding symmetry is fundamentally different. An electronic topological insulator is protected by the electron’s spin-1/2 (fermionic) time-reversal symmetry; however, due to photon’s spin-1 (bosonic) time-reversal symmetry, the same protection does not exist under normal circumstances for a photonic topological insulator. In other words, we could have a Chern photonic insulator with broken time-reversal symmetry. Time reversal symmetry broken topological phases provide gapless surface states protected by topology, regardless of additional internal symmetries, spin or valley degrees of freedom. Thus, the topology of the propagation of light in photonic crystals has been the subject of much recent attention.

Despite the numerous demonstrations of 2D topological phases, few examples of 3D topological systems with time reversal symmetry breaking exist. In contrast to 2D, a 3D Chern insulator is a topological phase that can be characterized by three first Chern invariants–or a Chern vector C = (C_x, C_y, C_z) – defined on lower dimensional surfaces: such a state of matter can support chiral surface states propagating on the planes with Miller indices indicated by the Chern vector.

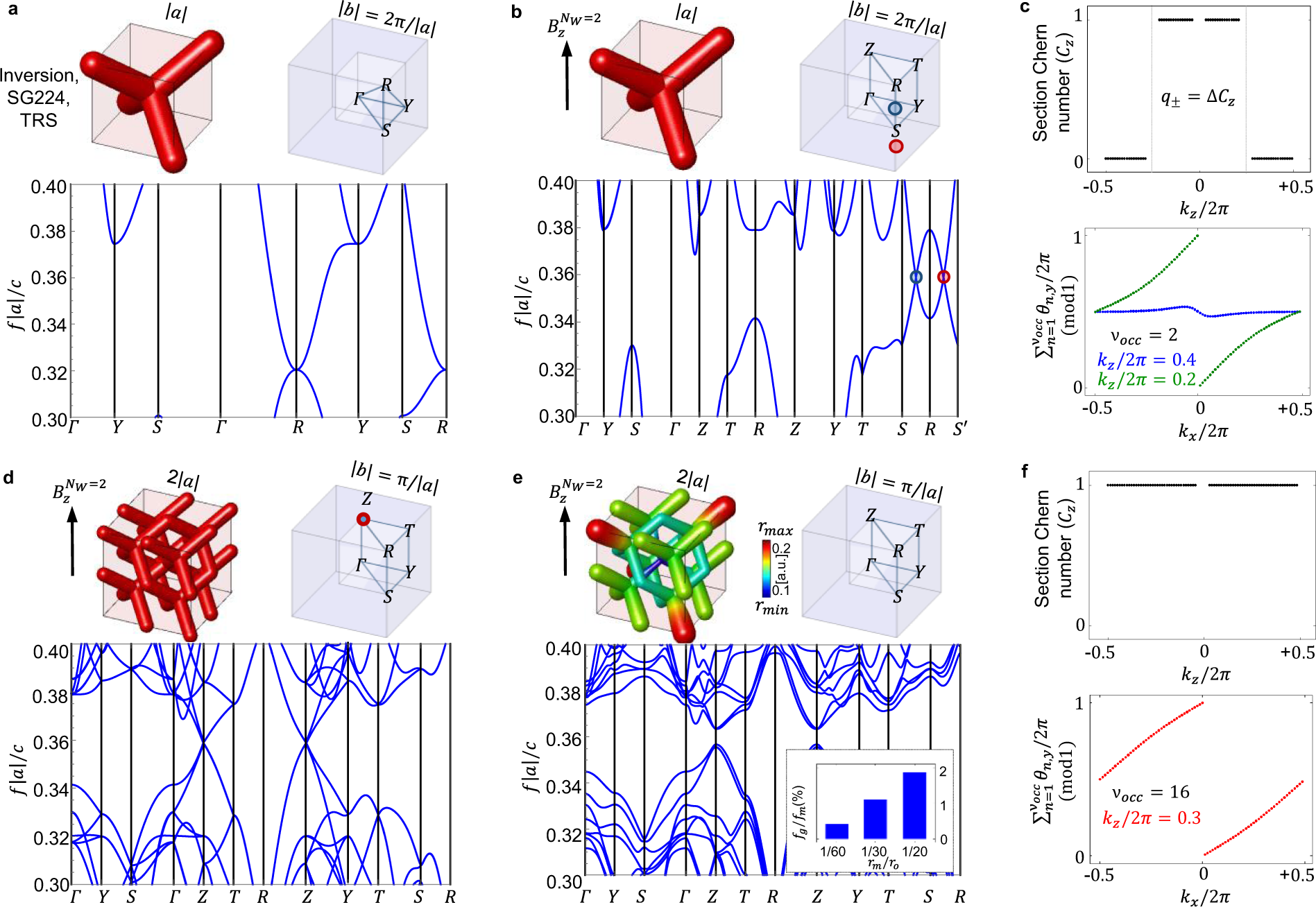
Now, a team of researchers proposes ¹ a method to design cubic 3D topological photonic crystals where Chern vectors of any magnitude, sign or direction can be implemented at will. The new method is based on the merging and annihilation of Weyl points through multifold supercell modulations in three dimensions. The designs achieved this way display topologically protected chiral and unidirectional surface states with disjoint equifrequency loops.

The resulting crystals present the following characteristics: First, by increasing the Chern number, multiple surface states channels can be supported. Second, the Chern vector can be oriented along any direction simply changing the magnetization axis, opening up larger cube/cube interfacing possibilities as compared to 2D. Third, by lowering the time reversal symmetry breaking requirements, the system is ideal for realistic photonic applications where the magnetic response is weak.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.