Topology as a parameter: an artificial electronic high-order topological insulator

Quantum simulators—systems that can be engineered and manipulated at will—are useful platforms for verifying model Hamiltonians and understanding more complex or elusive quantum systems. The ability to trap and control particles with the help of well-controlled electromagnetic fields has led to revolutionary advances in the fields of biology, condensed- matter physics, high-precision spectroscopy, and quantum information, enabling unprecedented control both in the study of isolated single particles as well as in few and many-body systems subject to controlled and tunable interactions. Prominent examples range from using optical tweezers for probing the mechanical properties of DNA to the realizations of Bose-Einstein condensates and numerous breakthrough investigations of strongly correlated quantum many-body systems with both trapped ions and ultracold atoms in optical lattices.

Still, progress on electronic systems was achieved only very recently. A few years ago, the first artificial electronic lattice was built by positioning carbon monoxide (CO) molecules on a Cu(111) surface, confining the surface-state electrons to a honeycomb lattice. This was followed by other electronic and spin lattices constructed by atomic manipulation in the scanning tunnelling microscope (STM), such as atomic spin chains, the Lieb lattice with s orbitals and p orbitals, the quasicrystalline Penrose tiling and the Sierpiński gasket with a fractional dimension.

In addition to manipulating the geometry and the dimensionality, it is desirable to engineer and control topological properties in electronic systems. Topological insulators, superconductors and semimetals have attracted enormous attention in recent decades, and their potential use in quantum computers has caused a frantic interest in these systems.

Topological insulators are materials with special universal properties, which are protected against perturbations. Such properties are theoretically described by topology, a branch of mathematics concerned with the properties of geometrical objects that are unchanged by continuous deformations. Concretely, topological insulators are electronic materials that have a bulk band gap like an ordinary insulator but have conducting states on their boundaries, i.e., edges or surfaces. The conducting surface is not what makes topological insulators unique, but the fact that this surface state is particularly robust, potentially due to some symmetry like time-reversal.

Thus, in general, we can say that a topological insulator of d dimensions with a given symmetry is insulating in the bulk but supports gapless boundary excitations that cannot be removed by local boundary perturbations without breaking the symmetry. Benalcazar et al published in Science ¹ a generalization of this bulk-boundary correspondence. In two and three dimensions, these insulators exhibit no edge or surface states, respectively, but feature gapless, topological corner excitations corresponding to quantized higher electric multipole moments. These are the so-called higher-order topological insulators (HOTIs), in which the topological states emerge in at least two dimensions lower than the bulk.

HOTIs have been experimentally realized in photonic, phononic, topolectrical circuit, microwave circuit and acoustic systems. As you can see an electronic system was lacking. Till now, when a breathing kagome lattice has been shown ² to be the artificial realization of an electronic HOTI.

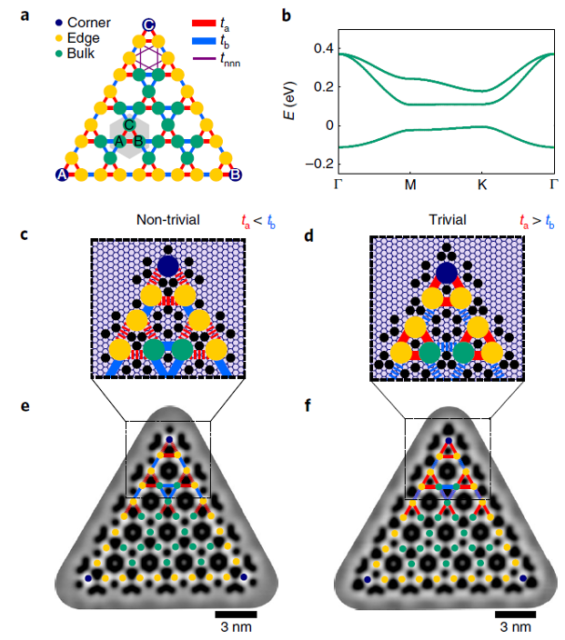
The researchers create the breathing kagome lattice by manipulating carbon monoxide molecules on a Cu(111) surface using a STM. They engineer alternating weak and strong bonds – this is the breathing – to show that a topological state emerges at the corner of the non-trivial configuration, but is absent in the trivial one.

Different from conventional topological insulators, the topological state has two dimensions less than the bulk, denoting a HOTI. Protected zero modes arise at the corners of the lattice, thus realizing a HOTI with extreme robustness due to the tripartite character of the generalized chiral symmetry. By introducing different types of defects into the lattice, zero modes can be manipulated at will, and the system can be tuned to have an even or odd number of corner modes.

The large degree of control over artificial lattices provides unique opportunities to study electronic topological phases. This new technique allows, in principle, the investigation of any breathing 2D lattice. Furthermore, it will be possible to study the interplay of topologically protected edge modes and edge geometry in topological crystalline insulators.

These electronic systems are thus complementary to photonic systems, which are designed on a much larger scale, and to the cold-atom set-ups, which offer great control but require nanokelvin temperatures for their operation. The progress in the realization of artificial electronic structures takes a step forward with the inclusion of topology among the parameters to be manipulated.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article are copied verbatim or almost verbatim from the referenced research paper.