Vortices and skyrmions in water surfaces

Numerous physical systems—from classical electromagnetic fields to quantum particle fields—exhibit oscillating wave behavior. Specific settings exist, both in nature and in artificial systems, where these waves form patterns with holes, loops, and other distinct topological characteristics, often referred to as topological wave structures.
Now, a team of researchers describes 1 how these structures, which have previously been observed in optical, elastic, and quantum systems, could be implemented in straightforward experiments based on water surfaces. Water waves might thus offer a practical platform for probing universal topological wave phenomena!
Wave vortices are universal physical entities with non-trivial topological and dynamical properties: quantized phase increments around point phase singularities and quantum-like angular momentum.
Examples of wave vortices are known since the 19th century. These have been observed and explored in tidal, quantum-fluid, optical, sound, elastic, surface-plasmon, exciton-polariton, quantum electron, neutron, and atom waves. Strikingly, wave vortices have not been properly studied in the most obvious example of classical waves: water-surface waves.
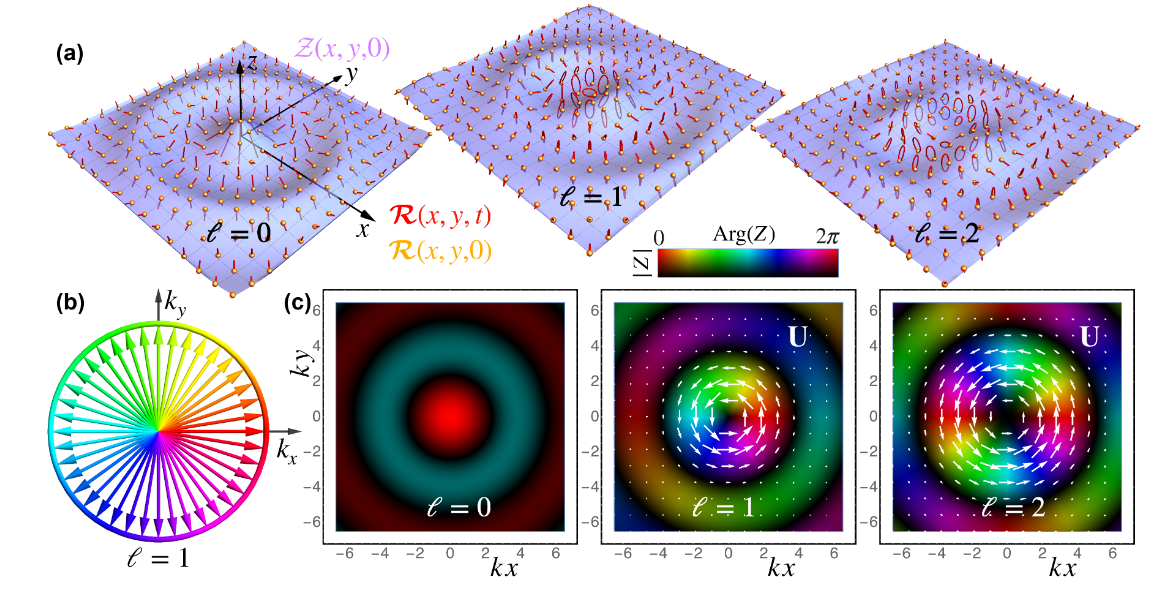
The researchers describe for the first time water-wave vortices in gravity-capillary waves. They reveal their topological properties and show that water particles experience two kinds of circular motions with different spatial and temporal scales: (i) local linear-amplitude-scale circular motion with the wave frequency in the linear regime and (ii) slow wavelength-scale circular motion due to the nonlinear Stokes drift. These two motions are responsible for the spin and orbital contributions to the quantized total angular momentum.
But water waves also have inherent vector properties. Thus, following recent progress in the generation of topological vector entities – skyrmions [25] – in classical electromagnetic, sound, and elastic waves, the team introduces water-wave skyrmions. They show that the interference of three plane water waves can generate a hexagonal lattice of: (i) water-wave vortices; (ii) skyrmions of the instantaneous water-particle displacements and (iii) merons (half-skyrmions) of the local spin density. Detuning the frequency of one of the interfering waves, moving lattices of spatio-temporal water-wave vortices and spatio-temporal skyrmions could be produced.
This way, new structures with remarkable topological and dynamical properties in linear water waves are revealed. The scientists argue that water waves now offer a perfect classical platform for emulating universal quantum and topological wave phenomena, which can also find useful applications in microfluidics.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.
References
- Daria A. Smirnova, Franco Nori, and Konstantin Y. Bliokh (2024) Water-Wave Vortices and Skyrmions Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.054003 ↩