How to calculate entanglement entropy using a Monte Carlo method

Entanglement entropy is a measure of the degree of quantum entanglement between two subsystems constituting a two-part composite quantum system. But entanglement entropy also quantifies the information shared between a subsystem and its environment in a quantum many-body wavefunction. Interestingly, the finite-size scaling form of entanglement entropy has contributions that depend uniquely on universal physical quantities, making it a powerful probe to characterize strongly correlated systems. A widely known example of this is found in one-dimensional critical systems, where entanglement entropy grows logarithmically in the subsystem size with a prefactor given by the central charge.

In two dimensions, things get more complicated. On one hand, the leading term of the entanglement entropy grows at most proportionally with the boundary of the subsystem, the so-called “area law”. On the other, if the subsystem contains sharp corners, critical ground states display a subleading universal logarithmic contribution.

Despite a wide variety of numerical work investigating spin and boson systems, the universal features of entanglement entropy of two-dimensional interacting fermions have remained, for the most part, an unexplored frontier. The pioneering work of Grover introduced auxiliary-field determinental quantum Monte Carlo (DQMC) simulations as a promising route to large-scale calculations of the Rényi entanglement entropy of interacting fermions. But the sampling from uncorrelated replica configurations make the estimator suffer from rare events that dominate the statistical average. Consequently, the universal features of entanglement entropy in 2D have remained out of reach for these methods.

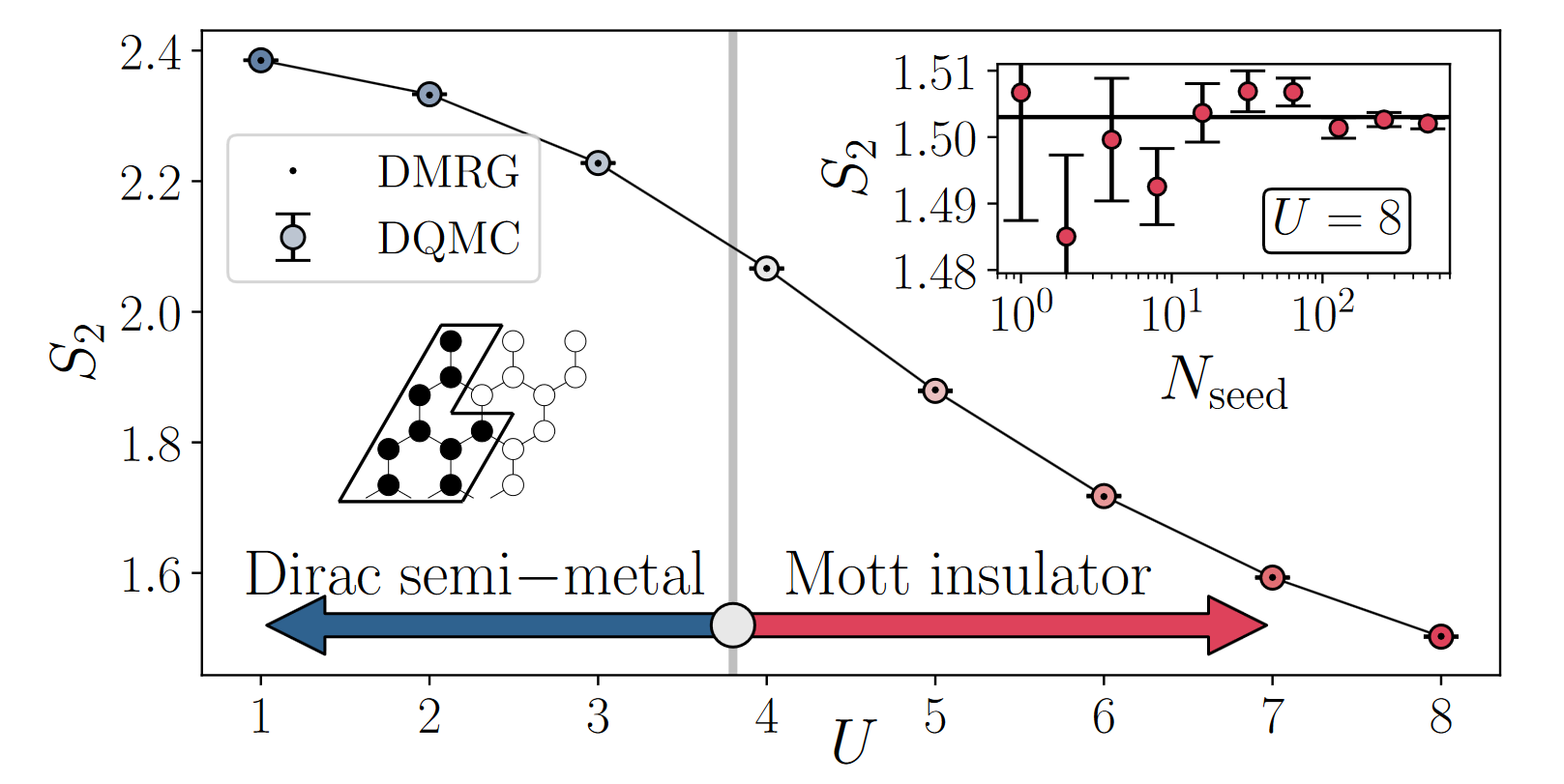
Now, a team of researchers presents ¹ an improved method to compute the Rényi entanglement entropy in DQMC that solves the above mentioned sampling problem and enables unprecedented precision. To do so, the team develops an improved equilibrium method for DQMC simulations.

The approach harnesses the power of importance sampling by introducing an extended ensemble of Monte Carlo configurations in which the entangling region is allowed to fluctuate. Remarkably, the original Grover’s formulation admits such an extended ensemble that can be simulated efficiently using standard DQMC techniques.

To demonstrate the power of this technique, the scientists use it to study a benchmark system, a classic model of interacting fermions in two dimensions, the half-filled honeycomb Hubbard model at T = 0. Doing so, they detect, for the first time, logarithmic corrections to the area law in a 2D model of interacting fermions. Importantly, they find that such logarithmic terms can be sensitive to the type of entanglement cut that is used.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.