The role of entanglement in quantum phase transitions

In a recent research, Jonathan D’Emidio and Anders W. Sandvik studied ¹ a property of quantum systems called Rényi entanglement entropy (EE) in a specific two-dimensional quantum spin model known as the J-Q model. This model is significant because it describes a type of deconfined quantum criticality, which occurs at a phase transition between two distinct types of ground states: the antiferromagnetic (AFM) state and the valence-bond-solid (VBS) state.

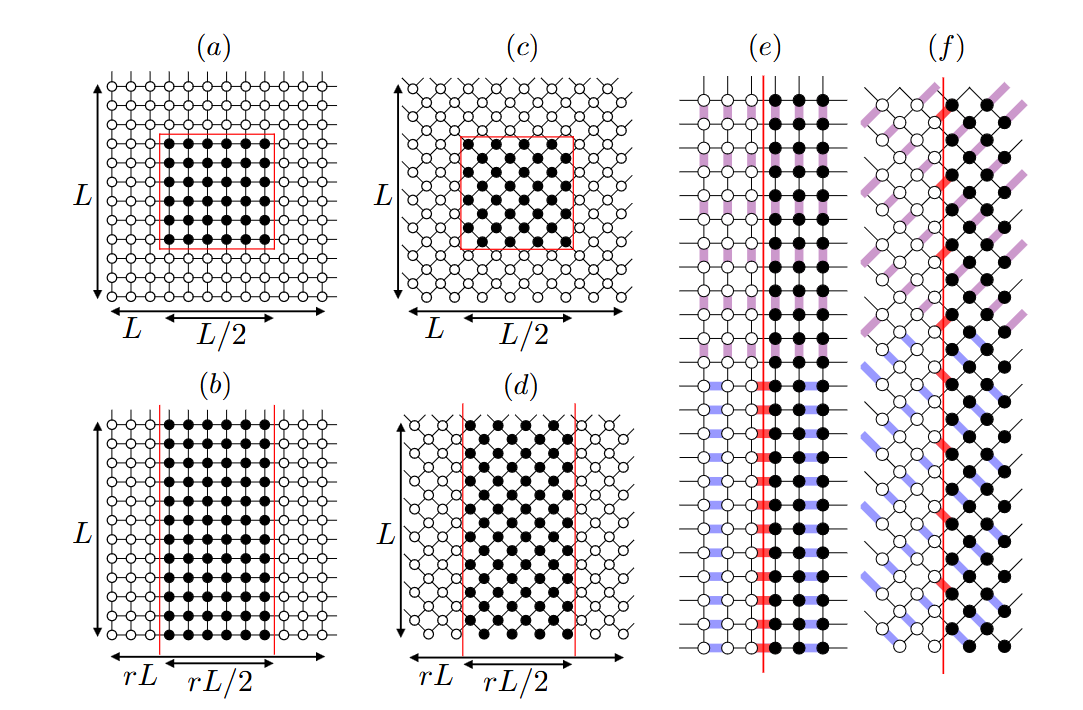
To understand what all of this means, let’s start with the concept of entanglement entropy. In quantum mechanics, entanglement refers to a situation where parts of a system cannot be described independently of each other. The entanglement entropy is a measure of how much entanglement there is in the system. For a quantum system, you can think of entangling two parts of it—this is called a bipartition. The EE quantifies the level of entanglement between these two parts. For instance, in a system with a large number of particles, the entanglement between different regions can tell us a lot about the system’s behavior and phase transitions.

Now, in the context of this study, they used quantum Monte Carlo simulations to compute the second Rényi entanglement entropy, which is a variation of entanglement entropy commonly used in quantum systems. What they found was that in the J-Q model, when the system is at the phase transition between the AFM and VBS states, there are logarithmic corrections to the expected scaling of entanglement entropy. These corrections are significant because they help us understand the nature of the phase transition. In particular, the coefficient of these logarithmic terms matched expectations based on conformal field theory (CFT), which is a framework used to describe certain types of quantum critical points.

Specifically, the match was with the form expected from a large-N CFT with SO(N = 5) symmetry, which suggests a deep connection to the underlying quantum-critical behaviour of the system. SO(N) stands for Special Orthogonal Group in mathematics, which describes a set of transformations (or symmetries) that involve rotations in N-dimensional space. The “special” part means these transformations preserve the orientation of the space, and the “orthogonal” part refers to the fact that the transformation preserves the distances between points. SO(N = 5) refers to the symmetry group of five-dimensional space. In the context of the J-Q model and the phase transition between the antiferromagnetic (AFM) and valence-bond-solid (VBS) ground states, this SO(5) symmetry is particularly significant. It suggests that the system has a certain type of rotational symmetry in a space of five dimensions, which is linked to the critical point where the AFM and VBS phases meet. SO(5) symmetry is often associated with deconfined quantum critical points (DQCP), like the one object of the study, because it reflects a situation where different types of order (like AFM and VBS) can be interchanged or “rotated” into each other without breaking the underlying symmetry. In simpler terms, at the deconfined quantum critical point, the system is not locked into one specific type of order (like the AFM state or the VBS state) but instead exhibits a kind of flexibility, where these orders can transform into each other in a way that respects the SO(5) symmetry.

In the new work, the researchers found that the logarithmic corrections to entanglement entropy at the critical point aligned with predictions from a large-N conformal field theory (CFT) with SO(5) symmetry. This further supports the idea that the phase transition between the AFM and VBS phases is governed by a quantum critical point with SO(5) symmetry, meaning the system has a rich, multi-dimensional structure where different orders can transform into each other symmetrically.

However, not all details of the bipartition were equal in their ability to reveal this behavior. A key finding from the study is that the way we divide the system matters a lot. If the subsystem (the part of the system we focus on) doesn’t properly take into account certain quantum fluctuations—specifically valence-bond fluctuations—then the logarithmic corrections can appear even if there are no corners in the bipartition boundary. This is important because the presence of corners in the way the system is divided has a major influence on the types of corrections we observe.

To ensure we properly capture the necessary behaviour, we used a 45° tilted cut across the square lattice, which allowed us to reveal the logarithmic corrections that come from the corners in the system. This tilted cut was crucial in seeing the effect of these corner contributions, and it also reinforced the idea that the phase transition between the AFM and VBS states exhibits the SO(5) symmetry that is central to the understanding of deconfined quantum critical points.

The study not only reinforces the idea that the AFM-VBS phase transition is governed by an SO(5) deconfined quantum critical point, but it also demonstrates how microscopic details of the system’s bipartition play a critical role in the observed entanglement behaviour. This highlights that there are aspects of entanglement entropy that are not captured by the conventional descriptions from conformal field theory. This work adds a new layer of understanding to the complex physics of quantum phase transitions and the role of entanglement in these phenomena.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.