Landau singularities revisited

Scientists have used computational algebraic geometry to study predictions for particle physics experiments, such as those at the Large Hadron Collider (LHC). These experiments, in combination with new mathematical tools, help to solve unanswered questions in physics in a much faster way and have a profound impact on our understanding of nature.

When studying particle collisions, physicists seek to describe the probability of particles arriving at certain states: whether they pass through each other, transform, or scatter at different angles, for example. This allows them to identify new particles or classify characteristics of existing ones. In order to do this, they must study particle interactions at the quantum level.

However, in quantum theory, it is impossible to predict the outcomes of particle collision with total certainty. Instead, physicists compute “scattering amplitudes,” which are mathematical expressions that encode the likelihood of different possible outcomes occurring when particles interact or collide. One of the characteristic features that physicists look for in these amplitudes are their “singularities,” which are points or regions where the probability amplitudes become infinite or undefined.

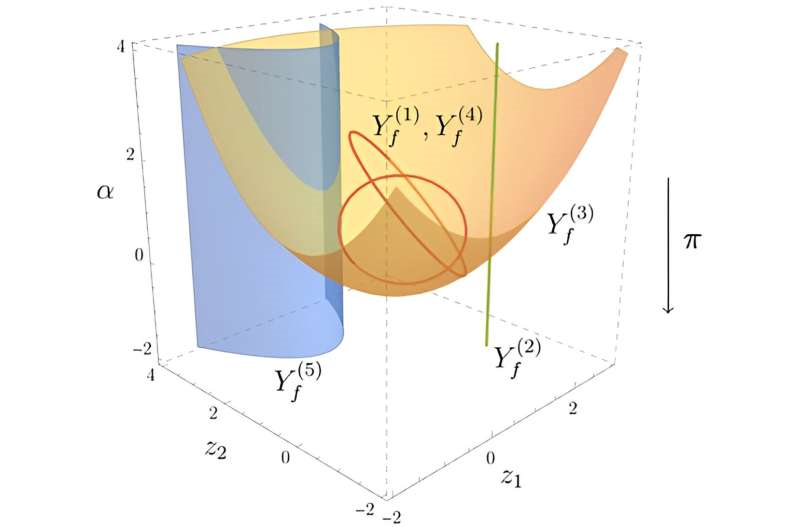
In this new work ¹, the researchers used mathematical tools including topology, geometry, and algebra to better understand a particular kind of singularity, namely Landau singularities. Landau singularities are geometric objects that quantify when virtual particles (those limited by the uncertainty principle) become observable particles.

By understanding the implications of Landau singularities, physicists can identify the energy scales and kinematic regimes where new phenomena, such as the production of new particles, may become possible. This plays an important role in interpreting and making predictions for experiments.

An algebraic variety called the “principal Landau determinant,” introduced by the authors in their paper, is likely to be even more helpful in this regard. The principal Landau variant finds singularities even in the presence of massless particles.

This is significant: locating singularities in the presence of massless particles is simultaneously the case most important to understanding the physics of the LHC and the most difficult to compute from a mathematical perspective.

This ability was demonstrated in the paper with a number of examples, including calculations needed to understand Higgs boson production in the presence of strong nuclear forces.

It is a major step in the ongoing progress by physicists worldwide to increase the high-precision computational capability used to verify predictions of the Standard Model of particle physics at the LHC.