The origins of neural variability

Neurons are known to display irregular behavior in many areas of the brain. When recording the evolution of the membrane potential of a given neuron in the prefrontal cortex (for instance, during in vivo electrophysiology), we can observe its erratic dynamics, with spikes occurring in a random and rather unpredictable fashion. This one and other neurons are connected forming large populations, which also display, in absence of an external input which could drive the response of the populations in a certain direction, a large degree of irregularity.
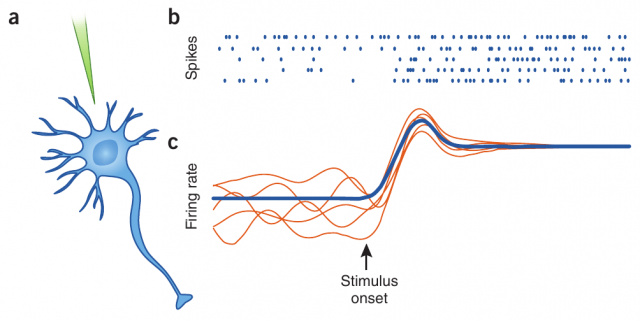
However, the membrane potential of this same erratic neuron presents a clean, predictable evolution when separated from its neighbor neurons. This is the case, for instance, when the recordings are done in vitro or in other controlled conditions. The origin of such irregularity is one of the great mysteries of modern brain science: how is it possible that deterministic and predictable units, once put together into a network, produce erratic behavior at so many different scales?
It is assumed that, at least, part of this puzzle was solved by Carl vanVreeswijk and Haim Sompolinsky, from the University of Paris V, in 1996 1, when they introduced the concept of balanced network and implemented it in a computer simulation of a neural network. The concept is based on the fact that neural networks are usually composed of excitatory and inhibitory neurons. While the signals coming from excitatory neurons tends to activate its neighbors and increase their firing rate, inhibitory neurons have the opposite effect, silencing the neurons that are connected to them and regulating the overall network activity.
In a balanced network, the strength of the connections between neurons is assumed to be very high, so that both the total excitation and the total inhibition arriving to a given neuron are enormous. However, since they have opposite effects, these signals roughly cancel each other, and the net input to the neuron is low. But since this cancellation is not perfect, the remaining small differences between both signals will constitute large fluctuations, which will originate the irregular firing activity of neurons observed in vivo.
Although this framework is able to satisfactorily explain the irregularity found at the neuron level in vivo, it is unable to explain the irregularity found at other spatial scales. For instance, the averaged activity of a population of neurons is hardly static, as it evolves in time in multiple manners, switching between different possible states, and displaying a prominent temporal variability, even in the absence of external signals (i.e. sensory input). Balanced networks, which tend to stick to a certain equilibrium state and remain there an undefined amount of time, do not provide a reasonable solution to this.
This second level of irregularity has been addressed recently by Ashok Litwin-Kumar and Brent Doiron 2, from the University of Pittsburgh, Pennsylvania. In this study, they propose a novel mechanism to justify this two-level (neuron and population) irregularity. In addition to the standard conditions of the balanced network, they have considered that, in real neural networks, neurons do not connect with each other in a purely random way. Indeed, after carefully analyzing the connectivity patterns of neural populations, it has been previously found that neurons tend to form clusters of highly connected neurons. Neurons within a given cluster are highly probable to establish connections between them, while establishing connections with neurons outside this cluster is much more rare. By introducing the existence of clustering into a biophysically detailed computer simulation of a balanced network of neurons, Litwin-Kumar and Doiron observed that the averaged activity of each cluster was not constant at all, but on the contrary, it was continuously changing and switching between different levels of activity, in resemblance with the variability observed in vivo. In addition, individual neurons presented an irregular behavior as in the case of a standard balanced network and as also observed in experiments.
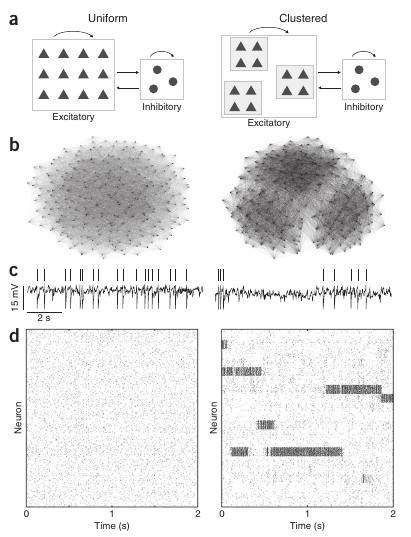
The computational model employed in the study was tested for other relevant situations as well. In particular, it is known that the averaged activity of a given population may decrease as external information arrives from the senses (or from other brain areas). This is pretty intuitive, since neural circuits have to respond fast and in an efficient manner to sensory information in order to allow, for instance, the animal’s survival. When the arrival of external information was simulated in the model, the researchers observed that the input was able to drive the response of the clusters by reducing the inner variability of the dynamics of the clusters and by pushing the network activity toward the desired output. This indicated that the proposed model was not only able to explain the spontaneous network dynamics, but also to perform well under the influence of external input mimicking relevant sensory information.
In summary, detailed computational simulations were exhaustively used by Litwin-Kumar and Doiron to demonstrate that the two-level irregularity observed in neural systems may be explained by the presence of two factors: clustering in the neural connectivity, and balanced input to the neurons in the network. Uncovering the origins of the neural irregularity observed at multiple scales could be a little closer now.
References
- C. A. van Vreeswijk and H. Sompolinsky. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724-1726, 1996 ↩
- A. Litwin-Kumar and B. Doiron. Slow dynamics and high variability in balanced cortical networks with clustered connections. Nature Neuroscience 15, 1498-1505, 2012 ↩
1 comment
Thanks very nice blog!