Advances on an Erdős problem on convex boundaries

By David Orden June 14, 2013 2 comments Print

Among his around 1525 papers, Paul Erdős considered On sets of distances of n points ¹ as his most important contribution to discrete geometry. There, he stated:

On the boundary of every convex body, there exists a point P such that every circle with center P intersects that boundary in at most 2 points.

(Note that throughout this post all the objects considered will be in the plane). This statement can be rephrased as:

On the boundary of every planar convex body, there exists a point P such that there are no more than 2 points equidistant to P on that boundary.

However, the conjecture turned out to be false. An easy counterexample is an acute triangle, for which any point on the boundary is the center of a circle intersecting that boundary in 4 points. The following figure shows this for a particular point, but you can check the points you want at this interactive GeoGebra construction.

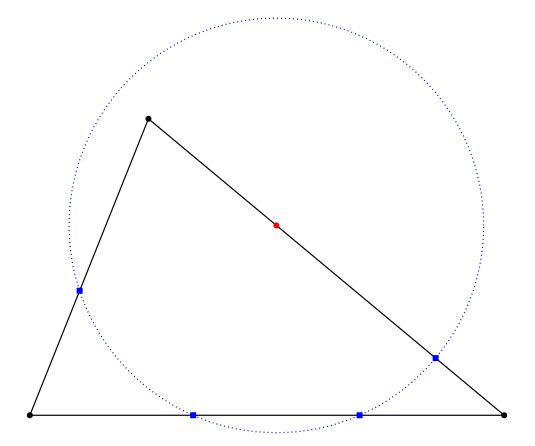
In fact, it turns out that any point on the boundary of a regular (2k+1)-gon is the center of a circle intersecting that boundary in 4 points. Naturally, a question arises:

Is this Erdős’s conjecture true when the upper bound 2 is replaced by 4?

Imre Bárány and Edgardo Roldán-Pensado give a negative answer to this question, constructing a convex body such that the smallest number for which Erdős’s statement holds is 6, i.e., such that for any point P on its boundary there is a circle with center P intersecting that boundary in 6 points.

The convex body they construct is a 15-gon. They consider the points $A1= (1000,0)$ , $A2= (906,114)$ , $A3= (645,359)$ , and $A4= (-498,871)$ , together with the points $B_i$ and $C_i$ , for $i\in\{1,2,3,4\}$ , obtained by rotating the $A_i$ ‘s around the origin by an angle of $2\pi/3$ and of $4\pi/3$ , respectively. The 12-gon defined by these points looks like this

Credit: Bárány and Roldán-Pensado (2013)

and it can be checked at this interactive GeoGebra construction. The union of the shaded regions in the figure contains the polygonal chain $A_4B_1B_2B_3$ and, using a technical lemma, this allows to prove that for any point $P$ in some neighborhood $V$ of the polygonal chain $A_4B_1B_2B_3$ there is a circle with center $P$ that intersects the polygonal chain $C_1C_2C_3C_4$ in at least 6 points.

Another technical lemma, together with the fact of the angle $\angle A_3A_4B_1$ being acute, implies the existence of a suitable point $A_5$ . By rotational symmetry, there also exist suitable points $B_5$ and $C_5$ , such that $A_i, B_i, C_i$ for $i\in\{1,2,3,4,5\}$ form the claimed 15-gon.

In view of this construction, Bárány and Roldán-Pensado ² conjecture that

On the boundary of every convex body, there exists a point P such that every circle with center P intersects that boundary in at most 6 points (i.e., such that there are no more than 6 points equidistant to P on that boundary).

It is interesting to note that, both the original Erdős’s conjecture and this updated one, state the existence of a universal upper bound for the number of intersections (or equidistant points), independent of the convex body considered.

Although the existence of such a universal constant remains open, Bárány and Roldán-Pensado throw some light on the problem. They prove that for every convex body there is a finite upper bound as in the statement. More formally:

For every convex body $K$ , there is an $N(K)$ being the smallest natural number for which there exists a point $P$ on the boundary of $K$ such that every circle with center $P$ intersects the boundary of $K$ in at most $N(K)$ points (i.e., such that there are no more than $N(K)$ points equidistant to $P$ on that boundary).

This finiteness result is actually a consequence of a stronger one. For a fixed convex body $K$ , one can define the set $\Gamma$ of pairs $(Q,\ell)$ in which $Q$ is a point on the boundary of the convex body and $\ell$ is a normal to that boundary at $Q$ . See the following figure.

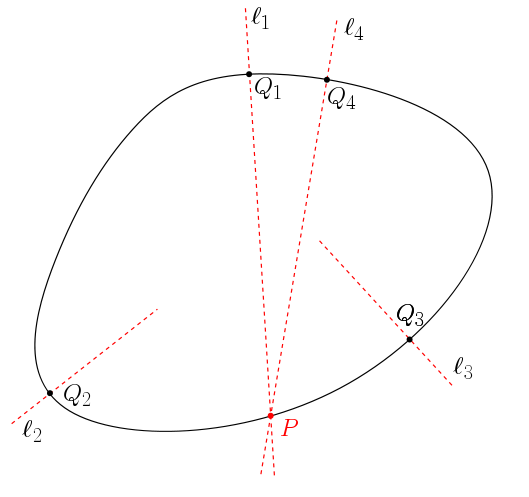
Note that there might be several pairs for which the normals intersect at a common point $P$ on the boundary of the convex body, like $\ell_1$ and $\ell_4$ in the figure. What Bárány and Roldán-Pensado prove is that there exists a point $P$ for which this can only happen a finite number of times. More formally:

Given a convex body $K$ , there is a point $P$ on the boundary of $K$ for which there is a finite number of pairs $(Q,\ell)\in\Gamma$ such that $P\in\ell$ and $P\neq Q$ .

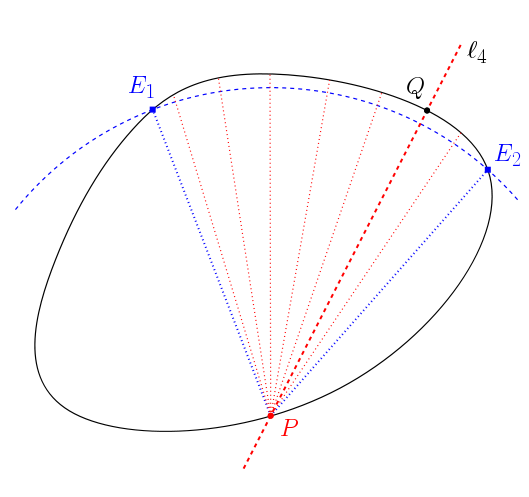
The reason why this result implies the previous one deserves to be explained before finishing. Consider a point $P$ on the boundary of $K$ such that there are 2 points equidistant to $P$ on that boundary, call them $E_1$ and $E_2$ . The distance between $P$ and these two points on the boundary is the same.

Hence, because of Rolle’s theorem, there must be a point $Q$ on the boundary, between $E_1$ and $E_2$ , which maximizes or minimizes the distance to $P$ . Then, for this $Q$ there is a normal $\ell$ which contains $P$ . See the following figure.

Hence, if $P$ is a point on the boundary of $K$ for which there are $M$ pairs $(Q,\ell)\in\Gamma$ with $P\in\ell$ and $P\neq Q$ , then any circle centered at $P$ intersects the boundary in at most $M+1$ points, which implies that $N(K)\leq M+1$ . If the latter is finite, the former has to be finite as well.

As a final remark, note that this result does not imply the existence of a finite universal constant. There might exist a family of convex bodies $K_n$ with respective constants $N(K_n)$ such that those $N(K_n)$ tend to infinity. In that case, no constant $N$ would be universal, since one could always find a convex $K_n$ for which $N(K_n)>N$ , i.e., for which that $N$ would not be valid.

In summary, this paper by Bárány and Roldán-Pensado includes two significant advances on an Erdős problem which, despite its simple formulation, remains unsolved since 1946.

References

Paul Erdős. On sets of distances of n points. The American Mathematical Monthly 53(5) (1946), 248-250. http://www.jstor.org/stable/2305092 ↩
Imre Bárány and Edgardo Roldán-Pensado. A Question from a Famous Paper of Erdős. Discrete and Computational Geometry. DOI: http://dx.doi.org/10.1007/s00454-013-9507-z ↩

2 comments

dramey

June 15, 2013

As far as I understand the conjecture says that there exists a point P, not that all the points have that special property. Therefore, I think that should not be stated that the conjecture is false because the example of the triangle.

Reply
David Orden

June 16, 2013

Dear dramey. Here comes another explanation, which I hope you find helpful.

Let us focus on the (boundary of the) acute triangle. What Erdős’s statement says is that there exists a “special” point P on the triangle, where special means having the following property:

“Every circle with center P intersects the triangle in at most 2 points.”

Why is this is false? For any P you choose on the triangle, the Grinch can find a circle centered on your P and intersecting the triangle in 4 points.

Thus, the Grinch has showed that for your point P:

“Not every circle with center P intersects the triangle in at most 2 points.”

because there is one intersecting in 4 points. In other words, the Grinch has showed that your point P is not “special”.

But the Grinch can do the same for any point P you choose, so there is no “special” point and hence the statement is false.

Of course, the counterexample is not mine, I just try to explain it 🙂 You can play around and emulate the Grinch with the GeoGebra interactive construction for the triangle.

Reply

References

2 comments

Leave a ReplyCancel reply

Leave a Reply