Down in the depths ‘on’ Carathéodory’s theorem
Research in general, and mathematical one in particular, sometimes reminds to the lyrics that Cole Porter wrote for the Down in the depths song:
And here am I
Facing tomorrow
Alone with my sorrow
Down in the depths on the ninetieth floor.

Nevertheless, sometimes you manage to get down in the depths and achieve a nice and/or remarkable result. The paper consider here achieves both, by extending a classical theorem in a clever and interesting way.
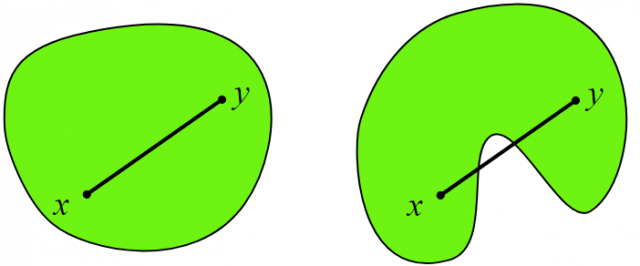
First things first, convex geometry is a branch of mathematics which, despite dating back from ancient times, has boosted particularly in the last century. Its main object of study are those sets being closed under convex combinations, called convex sets. In the more familiar setting of a d-dimensional Euclidean space (like the 2D-plane or the 3D-space), convex sets are then those for which the straight segment joining any two points is entirely contained in the set. The following figure shows examples of convex (left) and non-convex (right) sets.
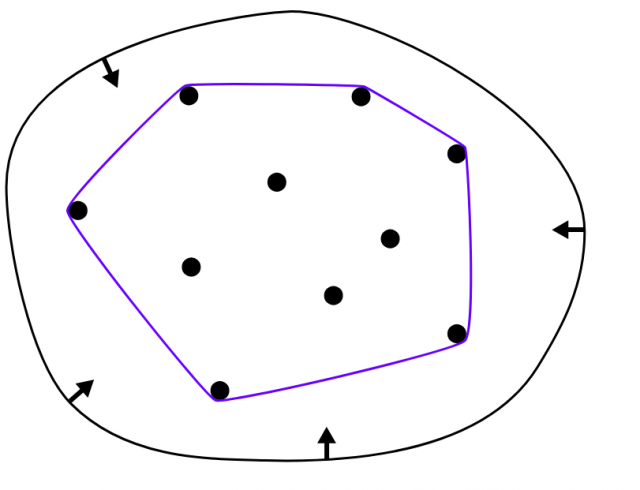
Focusing on discrete convex geometry, an outstanding notion is that of the convex hull, or convex envelope, of a given set of points in the d-dimensional space ![]() . This is the smallest convex set containing the points, and its computation is, for example, a central problem in computational geometry. Informally, for the 2D case we can see the convex hull as the result obtained if we surround the point set with an expanded rubber band, and then release it allowing its contraction.
. This is the smallest convex set containing the points, and its computation is, for example, a central problem in computational geometry. Informally, for the 2D case we can see the convex hull as the result obtained if we surround the point set with an expanded rubber band, and then release it allowing its contraction.
This simple notion of convex hull is the main ingredient for one of the outstanding classical theorems in convex geometry, proved by Carathéodory 1 in 1907, which states that
For any finite set
of points in
, given any point
contained in the convex hull of
, there exist
points
in
such that
is contained in their convex hull
.
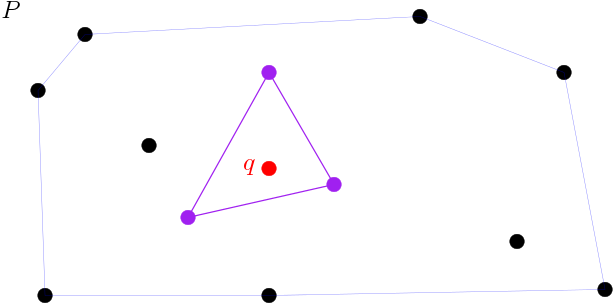
For the two-dimensional case, with ![]() , this means that given any point
, this means that given any point ![]() “inside” an arbitrary set of points
“inside” an arbitrary set of points ![]() , there are 3 points
, there are 3 points ![]() that contain
that contain ![]() inside the triangle they define. (Note that general position, i.e., no three points aligned, should be assumed for the triangle to be proper.) The result might seem trivial for this 2D case but be aware that geometry in higher dimensions is not so apparent and many counterintuitive situations arise.
inside the triangle they define. (Note that general position, i.e., no three points aligned, should be assumed for the triangle to be proper.) The result might seem trivial for this 2D case but be aware that geometry in higher dimensions is not so apparent and many counterintuitive situations arise.
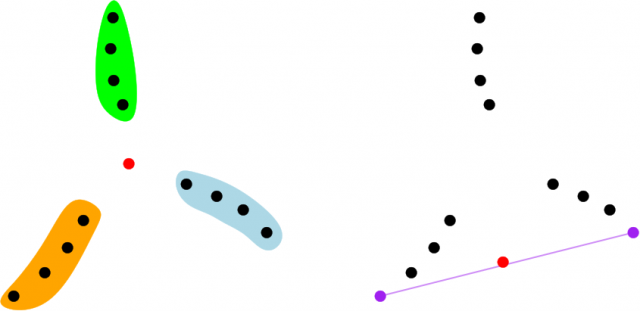
Back to intuitions, have a look at the left and right configurations in the following figure: Which of the two possibilities for ![]() (red point) do you think is contained in the larger number of triangles spanned by points in
(red point) do you think is contained in the larger number of triangles spanned by points in ![]() (black)?
(black)?

You probably have guessed that the configuration on the left should have more triangles containing ![]() than the configuration on the right: In the one on the left, choosing one point in each of the three blades of the windmill gives rise to a triangle containing
than the configuration on the right: In the one on the left, choosing one point in each of the three blades of the windmill gives rise to a triangle containing ![]() , that is, there are
, that is, there are ![]() such triangles. However, in the one on the right, since the point
such triangles. However, in the one on the right, since the point ![]() is just an epsilon over the lower edge of the triangular envelope, that edge is forced to be part of any triangle containing
is just an epsilon over the lower edge of the triangular envelope, that edge is forced to be part of any triangle containing ![]() , and actually the only possibilities are the
, and actually the only possibilities are the ![]() triangles using that edge plus an additional point.
triangles using that edge plus an additional point.
In view of the previous example, it seems that the deeper is ![]() inside
inside ![]() , the larger number of triangles can be chosen containing
, the larger number of triangles can be chosen containing ![]() . Formalizing this intuition is the main result in a recent paper by Fabila-Monroy and Huemer 2 who, 110 years later than the original paper by Carathéodory, have succeeded to prove the following result:
. Formalizing this intuition is the main result in a recent paper by Fabila-Monroy and Huemer 2 who, 110 years later than the original paper by Carathéodory, have succeeded to prove the following result:
For any finite set
of points in
, given any point
of positive depth
with respect to
, there is a constant
depending on
and there exist
pairwise disjoint subsets
of
, each of them with cardinality at least
, such that, for every choice of a point
in each of the subsets
, the point
is contained in the convex hull
of the chosen points.
Informally, this statement says that the deeper is ![]() inside
inside ![]() , the larger subsets
, the larger subsets ![]() exist such that choosing one point in each of them gives an envelope containing
exist such that choosing one point in each of them gives an envelope containing ![]() . In this sense, the original and classical Carathéodory’s theorem states the existence of sets
. In this sense, the original and classical Carathéodory’s theorem states the existence of sets ![]() with cardinality one, while this recent result goes further by ensuring certain cardinality which depends on the depth. In the left configuration of the example above, we have already seen three subsets of cardinality 4 as in the statement, namely the three blades of the windmill.
with cardinality one, while this recent result goes further by ensuring certain cardinality which depends on the depth. In the left configuration of the example above, we have already seen three subsets of cardinality 4 as in the statement, namely the three blades of the windmill.
There are actually many possibilities to define how deep is a point ![]() inside the envelope of a point set
inside the envelope of a point set ![]() . The notion of depth considered by Fabila-Monroy and Huemer is the so-called Tukey depth, defined as the minimum number of points from
. The notion of depth considered by Fabila-Monroy and Huemer is the so-called Tukey depth, defined as the minimum number of points from ![]() in a halfplane containing
in a halfplane containing ![]() . In the example above, the depth of
. In the example above, the depth of ![]() is 4 for the left configuration and 2 for the right configuration.
is 4 for the left configuration and 2 for the right configuration.
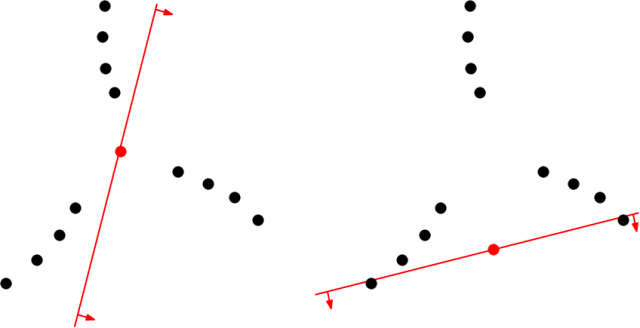
As their key ingredient, Ruy-Fabila and Huemer introduce the notion of projection Tukey depth of a point ![]() with respect to a set
with respect to a set ![]() and a hyperplane
and a hyperplane ![]() . Informally, a large projection Tukey depth means that there exists a direction
. Informally, a large projection Tukey depth means that there exists a direction ![]() in which
in which ![]() can be projected onto hyperplanes
can be projected onto hyperplanes ![]() and
and ![]() , parallel to
, parallel to ![]() on opposite sides, such that in the resulting configurations the point
on opposite sides, such that in the resulting configurations the point ![]() has large Tukey depth with respect to the projections of
has large Tukey depth with respect to the projections of ![]() .
.
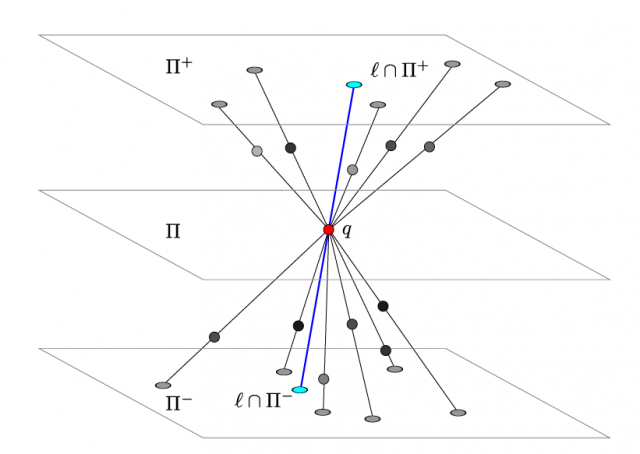
Defining the projection Tukey depth of a point ![]() with respect to a set
with respect to a set ![]() as the minimum over all the possible hyperplanes
as the minimum over all the possible hyperplanes ![]() , the authors prove a projection-depth version of the well-known centerpoint theorem (related to the geometric analogous of the median):
, the authors prove a projection-depth version of the well-known centerpoint theorem (related to the geometric analogous of the median):
Given any finite set
of points in
, there exists a point
, not necessarily in
, whose projection Tukey depth with respect to
is at least
.
Last, but not least, the authors also prove depth versions of two other classical theorems, namely Helly’s 3 and Kirchberger’s 4. As a summary, this work allows to revisit several classical and important theorems, providing at the same time a new and enriched perspective which enhances their deepness.
Note: This text is part of the dissemination activities of the Marie Skłodowska-Curie grant No 734922 in the European Union’s Horizon 2020 research and innovation programme.
References
- Carathéodory, C. (1907). Über den Variabilitätsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen. Mathematische Annalen, 64(1), 95-115. doi:10.1007/BF01449883 ↩
- Fabila-Monroy, R. & Huemer, C. (2017). Discrete and Computational Geometry, 58(1): 51-66. doi: 10.1007/s00454-017-9893-8 ↩
- Danzer, L., Grünbaum, B., and Klee, V. (1963). Helly’s theorem and its relatives. AMS ↩
- Kirchberger, P. (1903). Über Tchebychefsche Annäherungsmethoden. Mathematische Annalen, 57(4), 509-540. doi: 10.1007/BF01445182 ↩
3 comments
[…] Emaitza interesgarriak ditu geometria konputazionaleko klasiko baten hedapenak. David Ordenen Down in the depths ‘on’ Carathéodory’s theorem […]
[…] La extensión de un problema clásico de la geometría computacional da lugar a resultados muy interesantes. David Orden en Down in the depths ‘on’ Carathéodory’s theorem […]
[…] somewhat more mindbending maths, David Orden explains some new results relating to Carathéodory’s theorem, to do with the properties of a point chosen inside the convex hull of a set of other points, […]