Triangulations and face morphing

Face morphing has become quite popular in the last years; from mixing the faces of two celebrities to guessing how your baby could look, many TV shows and apps use software which changes one face into another through a continuous and smooth transition.

Among the different mathematical tools that can be used for face morphing, one of the easiest to understand is the morphing of triangulations. In this approach, a number of critical points are selected (e.g., the highest point of the nose, or the leftmost and rightmost points of the mouth) and a triangulation of those points is considered.

Back in 1944, Cairns ¹ proved that such a pair of triangulations, topologically equivalent, can be morphed one into the other while preserving planarity (i.e., avoiding segment crossings at the intermediate steps). The proof was by induction, based on contracting a vertex of low degree to a neighbor, and needed an exponential number of steps. It took almost 40 years until, in 1983, Thomassen ² extended the proof to all planar straight-line drawings, not necessarily triangulations. Nevertheless, the idea of this proof was augmenting those input drawings to isomorphic triangulations, and then using Cairns’ result.

Later in 1999, Floater and Gotsman ³ provided an alternative method for morphing triangulations based on Tutte’s graph drawing algorithm ⁴, further extended to all planar straight-line drawings by Surazhsky and Gotsman ⁵. A drawback of these algorithms is that they do not provide explicit trajectories for the vertices, computing instead a snapshot at the requested time points.

Finding vertex trajectories is precisely the achievement of a recent work on how to morph planar graph drawings, by Alamdari et al. ⁶, where each step is a unidirectional linear morph, i.e., every vertex moves at constant speed along a straight line (although the speeds of the vertices may differ). The authors succeed in obtaining an algorithm which uses only a linear number of steps, beating the exponential number in Cairns’ seminal paper, and they further prove that this complexity is worst-case optimal.

For an overview of the techniques, as above, the approach in the paper has two parts. First, solving the problem for the special case of triangulations, and then reducing the general problem for all planar straight-line drawings to that particular case of triangulations. For the case of triangulations, the idea is similar to the approach by Cairns: Finding a vertex that, in both triangulations, can be contracted to a neighbor while preserving planarity. This contraction provides two planar drawings of a smaller graph, for which recursion is used.

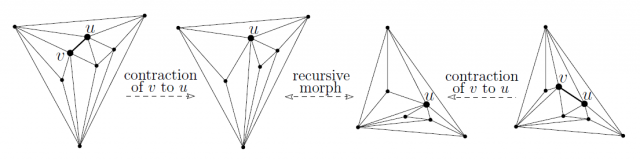
Such a plan has a couple of issues, the first one being that there might not be a vertex as above. The authors overcome this by choosing an interior vertex of degree at most 5 (which exists because of the graph being planar) and morphing the first drawing so that the neighbors of form a polygon such that one of them, chosen as , is able to “see” the whole polygon. Again, this mimics Cairns’ approach, but the authors manage to cut down his exponential number of steps to just two. The second issue is that the contraction should not make a vertex become coincident with another, but making them be close enough. Since Cairns’ solution resulted in a nonlinear motion, here the authors work out a different way of finding suitable positions.

For a bit of further detail, the core of the algorithm is a solution to the quadrilateral convexification problem: given a triangulation which contains a nonconvex quadrilateral, find a morph which makes that quadrilateral convex.

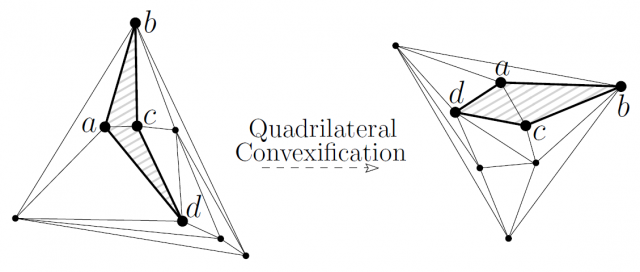
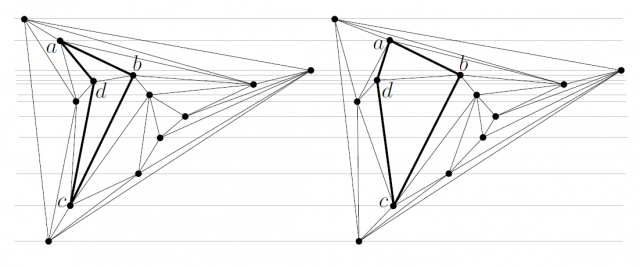
In order to do so, let be the vertices of the quadrilateral and we assume, without loss of generality, that is the reflex vertex of the nonconvex quadrilateral, i.e., the one with interior angle larger than 180 degrees. This implies that is the tip of the arrowhead shape of the quadrilateral and that the triangulation contains the edge (see the previous figure). Then, the authors change the frame of reference so that this edge is almost horizontal, so that they can use a result, by Hong and Nagamochi ⁷, which allows to redraw a plane graph, with only horizontal movements of the vertices, to achieve convex faces.

This paper by Alamdari et al., which collects the efforts of thirteen authors by combining four different conference papers, is a remarkable example of how collaboration can boost science further than competition to solve a problem with more than one century of history ⁸.

Note: This text is part of the dissemination activities of the Marie Skłodowska-Curie grant No 734922 in the European Union’s Horizon 2020 research and innovation programme.