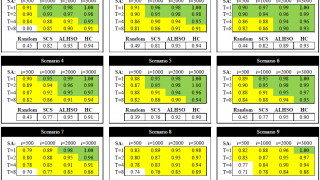
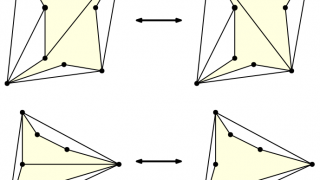
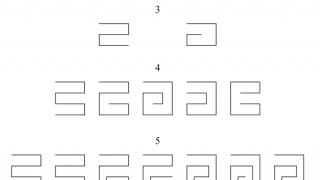
Sensory profiling is a very important tool in food industry, crucial in order to adapt the products to consumers’ preferences. Quantitative Descriptive Analysis (QDA) is a precise tool to relate characteristics of the product with consumers’ perception, since trained panels provide very detailed, robust, consistent, and reproducible results . However, creating and maintaining a well-trained […]
Research in general, and mathematical one in particular, sometimes reminds to the lyrics that Cole Porter wrote for the Down in the depths song: And here am I Facing tomorrow Alone with my sorrow Down in the depths on the ninetieth floor. Nevertheless, sometimes you manage to get down in the depths and achieve a […]
Face morphing has become quite popular in the last years; from mixing the faces of two celebrities to guessing how your baby could look, many TV shows and apps use software which changes one face into another through a continuous and smooth transition. Among the different mathematical tools that can be used for face morphing […]
Security in residential and public areas is a matter of great importance for many people. This is why some Internet providers are offering surveillance systems as a value-added service. Such surveillance systems have recently shifted from CCTVs to IP-based cameras, as the latter offer clear advantages to their users, like a more competitive cost and […]
This post is dedicated to the memory of Professor Ferran Hurtado , inspirational friend and colleague. Triangulations are extremely useful in computer graphics, with terrain modeling being an outstanding example: A mesh of points in 2D is triangulated and then the triangulation is lifted to obtain an -monotone polyhedral surface in 3D, called a 2.5D […]
Triangles are, definitely, among the most used mathematical objects. One of the reasons is that they are simple (actually the smallest polygon). Another very important reason is that they are rigid, which is the property behind the many structures composed by triangles we can see in our daily life. But, surprisingly enough, triangulations are not […]
We all know how Spider-Man moves through the city, shooting spider-webs from wall to wall. But, have you ever wondered if he is actually using the shortest route? And, if so, how does he compute it? Since walls introduce a third dimension into the problem, the algorithms in a usual GPS navigator are no longer […]
An old problem, restated by Martin Gardner in 1959, asked if six cigarettes that can be placed so that each touches the other. Gardner was surprised by fifteen readers discovering that actually seven cigarettes can be arranged with that condition . Some years later, in 1968, Littlewood raised the question if it possible in 3-space […]
When was the last time you used a postage stamp? Even if it was a long time ago, you may have hold in your hands a strip of stamps. Maybe you have even tried to fold it into a stack, one stamp wide, so that the strip was easier to store. Have you ever wondered […]
Imagine you are the owner of a hot dog stand and, after many stressful years in the streets of New York City, you are moving the business to the countryside. Of course, you want all the potential users to have your stand as close as possible. After thinking on it for a while, you take […]