The loophole-free quantum entanglement experiment (2): The locality loophole

In our previous post, we have discussed the importance of a loophole-free entanglement experiment. Now, we are going to discuss one of the most important loopholes for this kind of experiments, the locality (or communication) loophole12.
To understand the locality loophole we need to review the Bell’s inequalities experiments one more time. Alice and Bob will share two parts of the same quantum systems, and they will perform different measures on each part. After many repetitions, they share their results and calculate the average number of some quantities. They compute a new magnitude based on these averaged quantities and if the value is beyond a certain threshold there is a violation of Bell’s inequality and the universe should be either random (non-real) or it should allow some supraluminal communication (non-local). It sounds simple, but it is a little tricky. Bell’s inequalities are derived under certain assumptions, and we should verify that they hold for any experiment, mainly if this experiment pretends to be conclusive. The first of these assumptions is called locality.
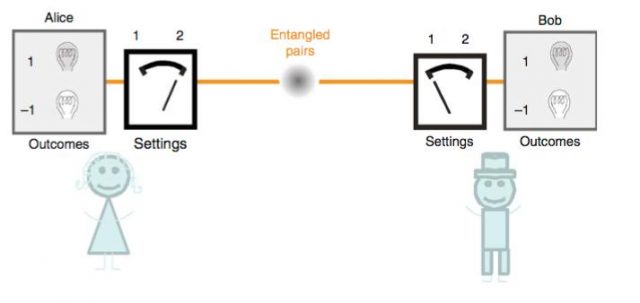
Alice and Bob should perform their experiment in a particular way. They should be in different labs, separated by a distance that ensures that in the time between their measurements light has not the time to travel from one lab to the other one. Using a relativistic phrasing, we can say that Bob’s measurements should be out of Alice measurements light cone. If the measures are performed too close, or in a too long time window, there is always the possibility of having classical communication between the two subsystems. We do not need to understand which kind of communication do they have. Just the possibility of having any kind of information travelling around ruins the conclusiveness of the experiment.
Conceptually it is very simple to solve the locality loophole. We only need to separate the two experimental setups and to perform the measurements in a small time window ensuring that light cannot travel between labs in such a small time. Unfortunately, light is really fast. Imagine that we have two labs separated by 10 meters. As the speed of light is 299792458 meters per second once Alice performs her measurement Bob has to measure in less than 0,000000033 seconds (or 33 nanoseconds). Furthermore, Alice cannot communicate Bob that she has performed her measurement, as classical communication is forbidden, they need to synchronize and to be sure that they perform their measurements in a very narrow time window. Distance should be higher.
This loophole was already present in Aspect’s first experiments3. It is also a ubiquitous problem in developing Bell-type experiments with trapped ions. Ions can be laser-cooled and use to generate entanglement in a very general way4. Unfortunately, even if this entanglement can be used to violate Bell’s inequalities it cannot disprove local-realism, as ions cannot be separated. Of course, this does not mean that this entanglement is useless. It can be used for many things as quantum computation and quantum teleportation, but it cannot solve our main question: if the universe is local and real.
As we have stated before the solution is simple, at least conceptually, we need to separate Bob and Alice’s labs. If we have ultrafast technology a distance of the order of kilometers could be enough to close the locality loophole. Doing this with ions is very complicated, because trap ions are not one kilometer long, so we need a quantum system with travelling capacity. Clearly, light is the natural option and the particles that form it, photons, are a quantum system that can be manipulated. By the use of optical fiber, we can separate both labs and send photons between them with minimum losses.
Hence, the problem is solved. Photons transmitted by optical fibers can do the job and close the locality loophole. This is certainly true. Unfortunately, in this case, when a door closes another opens. Even if transmitting and manipulating photons is easy, and there are very few losses, it is very difficult to couple optical fiber and photon detectors without losses. These losses are very important, and if they are too big the conclusions are again nondefinite. This problem constitutes the detection loophole, and it will be the topic for our next post.
References
- J-A Larsson. Loopholes in Bell inequality tests of local realism. (2014) J. Phys. A: Math. Theor. 47, 424003 DOI: 10.1088/1751-8113/47/42/424003 ↩
- C Brukner and M Zukowski. Bell’s Inequalities — Foundations and Quantum Communication. In Handbook of Natural Computing. Edited by G Rozenberg. Springer 2012. ↩
- A Aspect, P Grangier, G Roger. (1982) Experimental Tests of Realistic Local Theories via Bell’s Theorem. Phys. Rev. Lett. 47, 460 (1981). Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. Phys. Rev. Lett. 49, 91. ↩
- R Blatt and D Wineland. (2008) Entangled states of trapped atomic ions. Nature 453, 1008. ↩
2 comments
[…] por noesbasura | Feb 1, 2016 | Noticias, Physics, Quantum physics, Science | 0 […]
[…] La fantasmagórica acción a distancia, como la denominó Einstein, del entrelazamiento cuántico sigue siendo una de las características más paradójicas de la mecánica cuántica. Recientemente un experimento parece que ha levantado un montón de revuelo sobre este asunto, pero […]