Quantum measurement and the Arrow of Time

The question of the arrow of time has been on the table for centuries. The microscopic laws that determine the behaviour of matter (both in the classical and quantum regimes) are reversible. By seeing a video of a billiard board, with just a few balls, you will not be able to determine if the video is being played forward backwards. This usually changes when the number of particles increases. It is very easy to distinguish forward from backwards when you are breaking an initial position of sixteen balls. The reason for this distinction is purely probabilistic. There are many ways of breaking the rack, but very few combinations will end up forming the initial position again. Therefore, the backwards-in-time evolution is just unlikely.

Quantum systems are usually composed of a small number of components. Even so, the same argument can be used to define a quantum arrow of time. If we follow the interpretation of Quantum Bayesianism a quantum state is just a recipe to calculate the outcome of measurements. These measurements are performed by making the system interact with a bigger, more complex environment (the measurement device). Furthermore, as isolation is an ideal and complicated thing to get the system should interact with an uncontrolled environment, forming what is usually called a Quantum Open System. This may introduce some stochasticity in the system and, as in our billiard game, some outcomes will be more likely to occur. This fact helps us to define a Quantum Arrow of Time.

Recently, a superconducting circuit has been used in order to characterize an arrow of time in a quantum system ¹. This circuit presents two possible states, forming what is called a qubit, and it interacts with a radiation field. The radiation field can be monitored giving information about the system state.

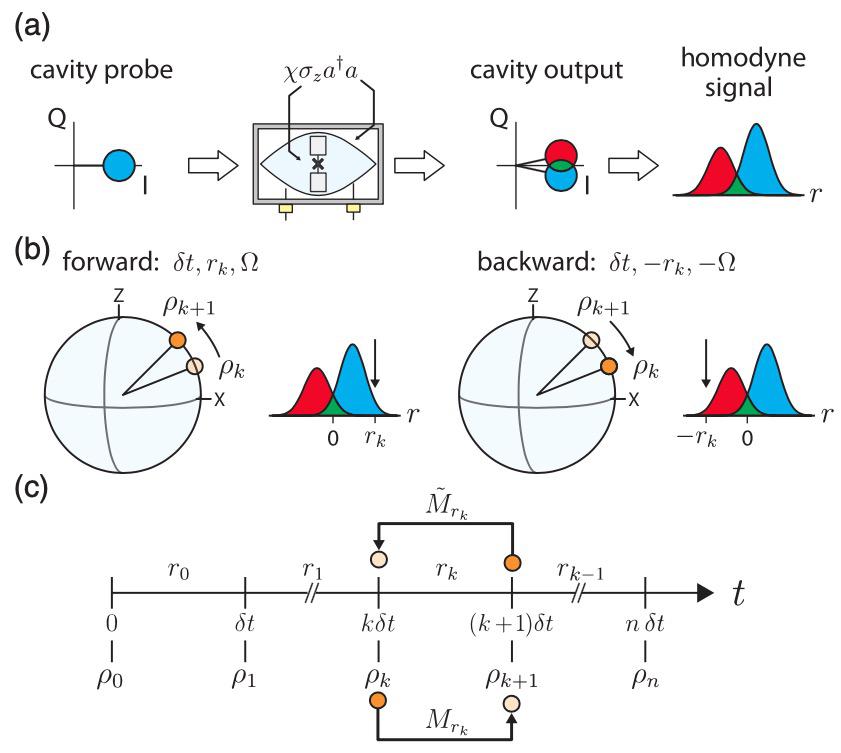
The measures performed in the system can be reversed, as well as the evolution of the system and the environment. For each trajectory of the system, defined as a series of outcomes obtained by the measures, the researchers define a magnitude that compares the probability of obtaining this trajectory if you are moving forward in comparison with the probability of having the same outcome if you are going back in time. This magnitude (Q), is bigger when a trajectory is more likely to happens in forward propagation.

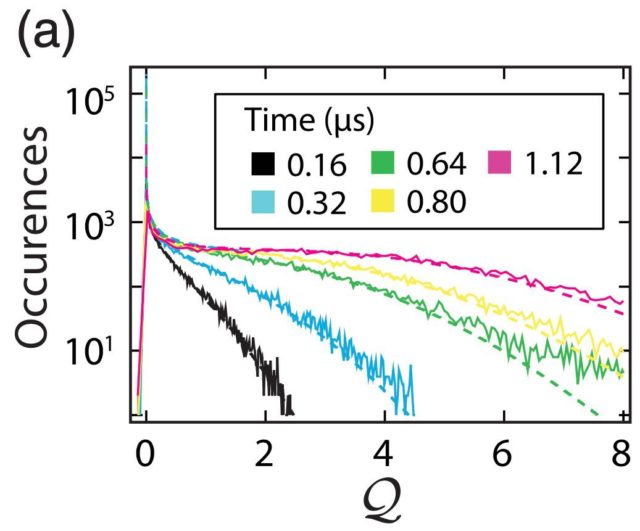
The experiment consisted of performing measures in the system with different time windows. In Figure 2 it is displayed the number of times a certain value of Q appeared in several experiments. There are almost only positive values of Q, meaning that the trajectories found are more compatible with a forward evolution than with a backwards one. Furthermore, when the time windows are made bigger, the system interacts with its environment for a longer time, and this makes higher values of the Q parameter more likely.

Coming back to the billiard simile, monitoring the trajectory of a quantum system cannot tell you if it is going forward or backwards, but it can give you the chances of these two options.