The loophole-free quantum entanglement experiment (5): The Delft experiment

In previous posts, we have reviewed the different loopholes of Bell experiments. To make a long story short, entanglement experiments are based on measuring some magnitudes in two quantum systems, calculating a value based on the outcomes of these measurements, and if this value goes beyond a certain threshold we can say that the universe is either non-local (there is faster than light communication) or non-real (the magnitudes were not defined before we measured them). Unfortunately, the inequality violation is not enough. To obtain a conclusive result two extra conditions should be imposed. First, the systems should be far enough to each other to ensure that there is no communication between them in the time between measures. Second, we need to measure at least three fourth of the events to ensure that our statistics is good enough. Researchers have been performing this kind of experiments since the eighties, but only recently someone claimed to have solved these issues.

It happens sometimes that after decades of pursuing a goal two different people, or groups, solve it in different ways in a short time window. This is one of these occasions. In less than four months two different groups claimed to have performed a loophole-free Bell experiment. The first experiment was lead by Ronald Hanson and the second one by Anton Zeilinger. In this post, we are discussing the first one. The experiment was performed in Delft University of Technology ¹ and it was a collaboration between researchers from The Netherlands, Spain, and the United Kingdom.

First of all, as we explained in the post about the locality loophole, a conclusive experiment needs two different labs (A and B) separated at least by several hundred meters. In this specific experiment, the separation was 1,280 meters, enough to close the locality loophole. The systems used to transfer the information were photons created in a third lab (C) and then sent to A and B by an optical fiber.

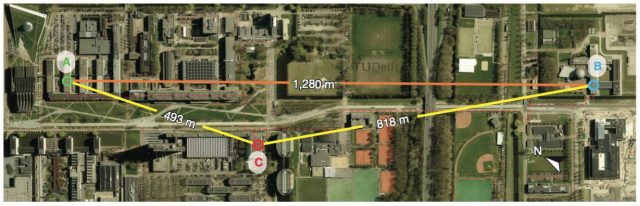
Photons are fast enough to ensure a closing of the locality loophole, but as we have discussed before they are easily lost. This makes difficult to close the detection loophole as we need to measure at least a 75% of them. To avoid this difficulty the researchers used an imaginative technique. Instead of measuring the photons directly, they first transfer their entangled state to a different kind of system. These new systems are called NV-centers, and they are composed by electronic spins at the center of diamond chips.

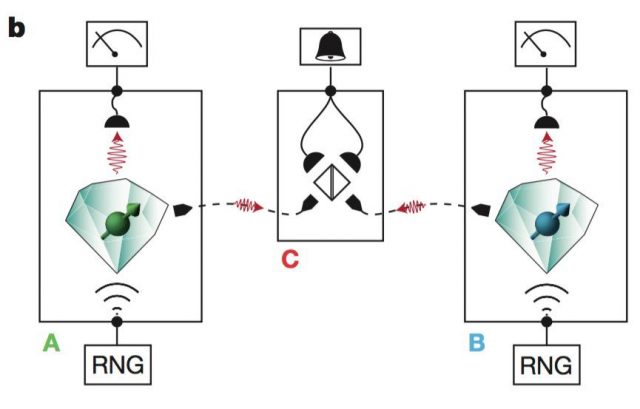
To transfer the state of the photons to the NV-center they used a technique called entanglement swapping ². By the use of this technique, one can transform the entanglement between two quantum systems to entanglement between two new systems. Therefore, one can transform two entangled photons into two entangled NV-centers.

One can ask then about the efficiency of the entanglement swapping protocol. It is indeed very low, but it does not really matter. The detection loophole only concerns to the measurements performed in order to check the Bell inequality. The procedure is clear then, we send the photon, we perform the entanglement swapping and if it works we measure the Bell magnitudes in the NV-centers. Most of the time the entanglement swapping does not work, but in this case, we only need to not measure the NV-center. The experiment run for 220 hours with 245 trials. They measure a value of 2.42 where the Bell inequality states that a local-deterministic theory cannot give more than 2.

This is considered the first experiment to show a loophole-free Bell inequality violation, but it is not the only one. Only two months after the publication of this paper Anton Zeilinger published a new one closing all the loopholes in a different way ³.