The Holy Spirit game, or a sip of conclave economics

Imagine the following situation: about 100 people have to choose one of them for an important position; they have different preferences about who must be chosen, some may have a stronger or lighter interest in being elected, but, and this is essential, it is very likely that most of them will have to cast their votes for candidates that are not the most preferred by them, because the election rule demands that the elected man (yes, there are no women between the electors neither between the eligibles) receives at least two thirds of the votes, and it is almost sure that no individual is the most preferred one by so many of his colleagues. This is, to say the least, an interesting problem to be studied from a game theoretic point of view: what game-theoretic properties the ‘solution’ of this problem is expected to have?

In a sense, the situation is similar (though obviously not identical) to that faced by the members of a scientific community having to choose which one is the best explanation of a scientific problem. In this case, it also happens that every scientist will probably have a different preference between alternative theories, and in particular if one of those theories has been proposed by her, but in the end, she will take into account to some extent the judgments of her colleagues as reasons to adopt one of those solutions even if it is not the most preferred by her. I analysed a situation like this in some academic papers and in my book La lonja del saber (‘The bazaar of wisdom’)¹²³.

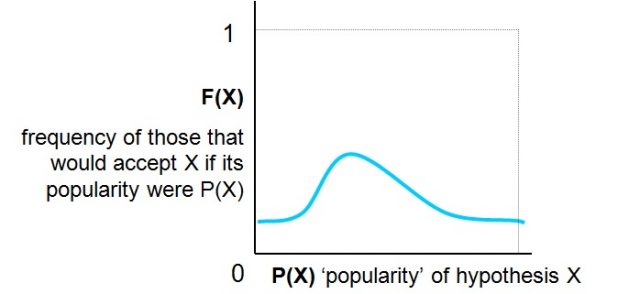
So, let’s be X one of the possible elections (one man, in the first case, one theory in the second), and let P(X) stand for the proportion of electors that chooses X. For every elector there will be some value of P(X) such that he (let’s go back to the man-only situation) would change his decision from not choosing X to choosing it; if this value for you is very low, this means that you will vote for X even if it is not chosen by many of your colleagues; if it is very high, it means that you will be reticent for voting in favour of X, save if it is supported by a big number. The distribution of the frequencies (F) of these ‘threshold values’ can be assumed to be more or less ‘normal’ (unimodal) around some median value that, for different candidates, will be more to the left or more to the right, as in the example of figure (1).

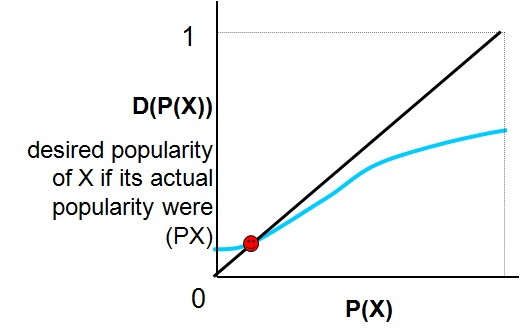
Figure (2) simply transforms the frequency function F into an accumulative function P, meaning what proportion of electors would prefer to vote for X, if the actual proportion of electors voting for X were P(X). Obviously, if F is unimodal, P will be S-shaped, i.e., convex at the beginning, and concave at the end. The question is, does function P contain enough information to determine the actual behaviour of the electors? Well, it depends. Take into account the 45 line (i.e., the function P(X)=P(X)). If P is over that line, this means that the number of people willing to vote by X is higher than the number of people actually voting by him, so, in the next election round, probably more people will vote for X. The opposite happens if function P is below the 45 line: some people will be not happy with having voted for X, and probably in the next round they will not. This means that the only equilibrium (in game theoretic terms) is where P and the 45 line cross. Of course, if this happens for a value of P(X) that is lower than 2/3, new rounds of elections will be necessary, and some people will have to re-consider their preferences.

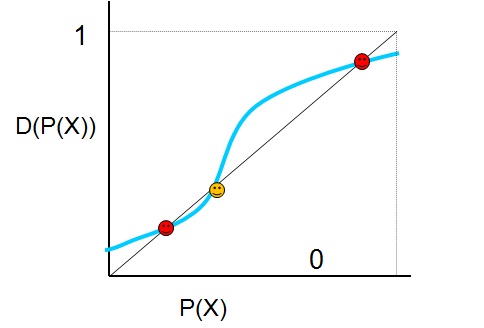
But an important problem is that, being the function P S-shaped, it can have three different equilibria, as shown in figure 3. What determines which one of them is actually taking place is simply history: if the previous situation of P(X) is one that falls between the origin of the horizontal axis and the second equilibrium, the dynamics sketched in the previous paragraph will tend to move the election towards the first (lower) equilibrium; whereas, if the previous situation was one falling between the second equilibrium and the maximum value of the axis, the same dynamics will move the election towards the third (higher) equilibrium. Of course, if the previous situation was exactly the middle equilibrium, it will rest there, but it is an unstable equilibrium (the slightest chance in preferences or behaviour will move the group up or down).

The possibility of more than one equilibria is not only a theoretical curiosity, but an important practical problem, for it can have some undesirable consequences. One of this consequences is that the result of the election will depend too much on mere chance; since this result depends on history, the results of the first (more or less blind) votations will determine in excess the result of the final election. This is a typical example of the ‘butterfly effect’ (in this case, it would be more appropriate to talk of the ‘dove effect’, for obvious reasons): a very slightly different result in the distribution of irrelevant candidates, can lead to the final choice of a different candidate.

But it is also worse than this. In fig. 4, the functions corresponding to two different candidates are shown. It is assumed that all the electors consider candidate A better than candidate B; this reflects in the fact that, for any given number of votes actually received, there will be more people preferring A than people preferring B. But even if this is the case, it can happen that more people choose B than A, for, though both stable equilibria of A are higher than the corresponding stable equilibria of B, it can be the case that the higher equilibria of B and the lower equilibrium of A are chosen. Hence, the group may end choosing a candidate that every member of the group considers to be worse than another particular candidate. Stated in economic terms: the election mechanism can lead to inefficient results.

Fortunately, it can be proved that, if the members of the group can form coalitions, i.e., sub-groups that adopt the commitment to cast their votes to the same candidate no matter what the rest of the electors do, then only one of the stable equilibria (in cases there are two) will remain stable. The problem with these coalitions is that, until the dynamics has led to that equilibrium (i.e., while the actual value of P is still different from the desired value of P), some members will individually prefer a different result, and will have an incentive to frustrate the coalition strategy, which is even more likely if the vote is secret.

In comparison to the case of the choice of a solution for a scientific problem, some other problems can be identified. More importantly, in the case of science, there is no pressure to make a choice in a relatively short time, individual decisions are public (not secret), and more and more information is usually accumulated in favour or against each proposed solution (when one of these becomes much more consistent with the data than the rest, persuading more and more people of its superior validity, its corresponding F function will displace towards the left, P towards the right, and only equilibrium, near the right upper corner of fig. 3 will remain). So, there is less space for random fluctuations of the equilibria, and more space for public, rational deliberation leading to ‘coalition’ voting. Perhaps if the Holy Spirit had thought a little bit more about the mechanism of choice we have been examining, It(?) had chosen a different one. Or perhaps what happens is that It prefers a more chaotic one, in which there is a more prominent role for Its (untestable) intervention.