Invertebrate mathematicians

It is happening again, right now. In multiple localities across Eastern North America, as the end of the spring warms up the soil, legions of hundreds of thousands of insects are being awakened from their underground hides. They reach the surface at night, climb up to the trees, and moult for the last time in their long (but mostly monotonous) life. During a very intense bunch of days as adults, they will countervail their silent and discreet juvenile period with a deafening mating call that will not stop until their equally mass and synchronic death. Hopefully, many of them will breed before that happens, and millions of minute eggs will be waiting inside branches and twigs. The next generation of cicadas will repeat the same spectacular performance… in the year 2030.

Periodical cicadas (genus Magicicada) have attracted the interest of very different type of people, from amateur entomologists to mathematicians. They do not seem very different from the cicadas of other parts of the world: all cicadas have a similar hemimetabolic life cycle with the nymph instars living for a long time underground, sucking the roots’ sap, and the winged adults contributing to the summer’s soundtrack. However, two traits make the Magicidada ¹ species distinct to any other kind of insect: the highly coordinated “outbreak” of adults and the unique regularity of their life cycles, restricted to 13 or 17 year periods.

The ecological significance of a synchronized emergence of adults may be rather easy to understand. Many animals from very different lineages (including annelids, mollusks, arthropods or vertebrates) experience a intense single reproductive event in their lives (this is called semelparity, or “big bang” reproduction) and often a particular geographic area becomes crowded with individuals, eager to mate and reproduce, frequently followed by a mass concentration of dead bodies. One of the advantages that it is often claimed for this strategy is that the organisms are protected from predators by their huge number: they are so many that the predators become satiated soon and they do not have a major impact on the population. In fact, a study on the mortality of periodical cicadas¹ confirmed that high density populations of these insects (over 24,000 individuals/ha) is not significantly affected by bird predation.

The regularity of the life cycles (13 and 17 years) raises much more complex questions that are not completely answered yet. To begin with, these cicadas show the longest life cycles within insects, which is already a remarkable fact. They remain hidden and safe for more than a decade, and synchronically emerge together to the surface for a short time to be protected from predators, as we just saw. A significant pressure may be behind this “fugitive” lifestyle, and the importance of a regular and predictable length of the juvenile period is essential for the success of the semelparous strategy, but why 13 and 17? Why not 12, 15 or 18? Why, among all the possibilities, only these are observed in nature? The fact that both are a prime number of years makes very hard to believe that it is just by chance.

We still have a lot of open questions regarding the 13/17y cycles, but one of the classical explanations is, again, related to avoiding predators. One may think that predators developing a multi-year periodical cycle may enjoy the feast of their lives if they match their cycle with the cicadas’. A prime number cycle would be more difficult to match by periodical predators. If the predator has a 10y cycle and the cicada a 15y cycle, a huge cicada genocide is likely to happen each 30 years once predator and prey got their cycles matched once. However, having a prime-number year cycle minimizes the chances of this contingency: a periodical predator can only take advantage of a regular 17-year-scheduled cicada barbecue if it has exactly a 17y life cycle… or a lot of patience, being an annual species. Mathematical simulations have verified that, at least theoretically, 13y and 17y cycle strategies are the most successful in different scenarios of quasy-cycling (i.e. periodical yet somewhat variable) predator population models².

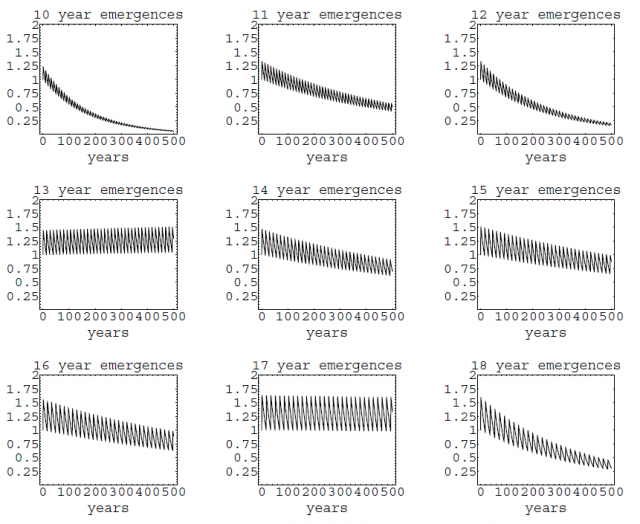
An alternative hypothesis that is gaining credit among specialists is that synchronized 13y and 17y cycles would work as a mechanism of stability, homogenizing the populations and preventing the population decay linked to the Allee effect during harsh periods, such as glaciations. (The Allee effect is a phenomenon that consists on a reduced offspring production when the population density is too low and finding a sexual mate becomes unlikely; ultimately it may lead to the extinction of the population). When simulations were run under a strong Allee effect, prime-numbers based cycles turned out to be more likely to persist and survive extinction³.

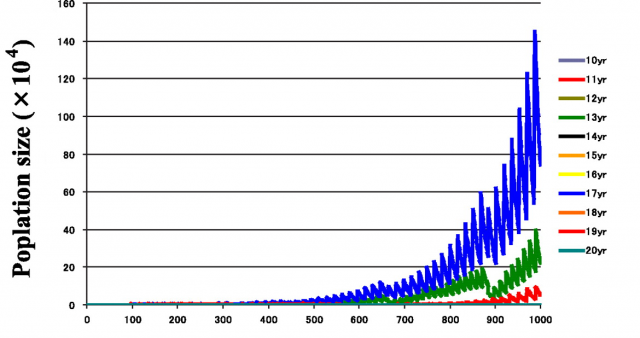
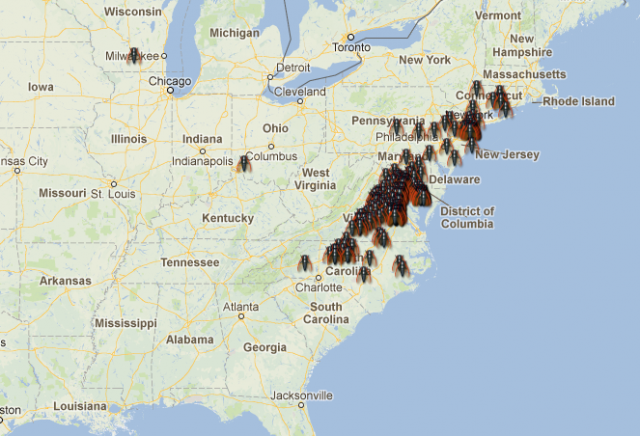
But the “why” is not the only issue. When and how did these cycles evolve? How stable are them? Answering these other questions requires a deep knowledge of the genus Magicicada and its evolution. Until now, we had access to a part of this knowledge: the result of many decades of entomological observations. If we consider together the 13y and the 17y cycles, up to 30 different broods could be expected. Many of these theoretical broods have never been observed, and others are known to become extinct in recent historical times. For all the existing broods (identified with roman numerals) there is a quite detailed record of where and when expect an occurrence of one of these invertebrate armies, and this is one of the most enjoyable characteristics of this biological phenomenon! For instance, the emergence that is active right now is known as the brood II, a 17y brood, and its distribution spans mostly from Connecticut to North Carolina, following the Appalachians. Complete information about broods of periodical cicadas can be found at the webpages Cicada Central or Cicada Mania.

Since each brood seems to be reproductively isolated, one would expect some kind of correlation between the morphology or phylogeny and the different life cycles. Surprisingly, this is not the case. Three different morphospecies are diagnosable within the genus, called Decim, Cassini and Decula; each of them showing a distinct behavior and song. None of these forms is characterized by a particular cycle; both, the 13y and the 17y can be observed in any of the morphospecies. This means that during any given brood, up to three different forms can be found. Just in case you are wondering: the combination of the cycle and the form name yields to the formal species names, such as Magicicada tredecula (13y cycle and Decula form), or M. septemdecim (17y cycle and Decim form). A number of factors that I have not mentioned makes this system even more complicated: spurious broods, rare off-schedule emergences and recently described new species. How should all this information be addressed?

Assuming that “nothing in biology makes sense except in the light of evolution”, a phylogeny of Magicicada would be a very useful tool to unravel this mistery overdose. This is not an easy task considering all the different broods and morphospecies that exist and how distant they are in time and space. Finally, a phylogenetic reconstruction of the genus, comprising all the species, all the broods and a wide geographic range was recently published^4,5, and it turned out that the cicadas were still keeping more secrets.

Consistently with the taxonomists’ results, three main clades, corresponding to the Decim, Cassini and Decula morphospecies are the highest ranked groups. Unexpectedly, a very similar, highly structured geographic pattern was nested within each of these clades: all of them have experienced a parallel evolution, yielding to three regional lineages comprising the Western, Central and Eastern distribution ranges. Only within many of these individual regional lineages is where we (finally!) find cladogenesis events segregating 13y and 17y cycles.

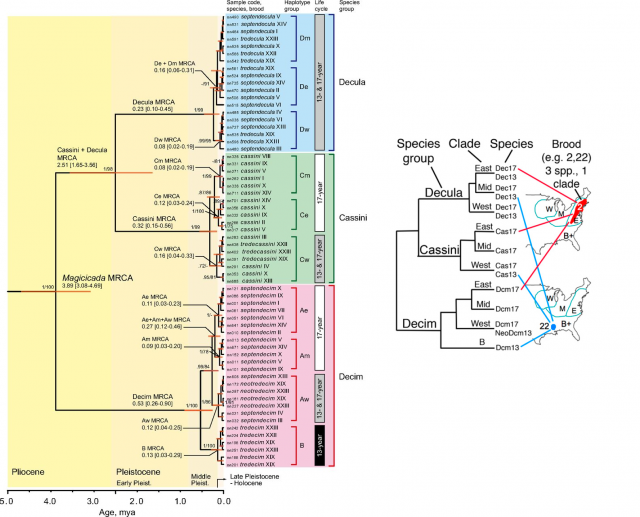
What does this mean? Shifts between 13y and 17y cycles are shamelessly frequent in the evolutionary history of Magicidada. They impress us with their mathematical precision, but apparently there is no big deal with them. Parapatric differentiation combined with life cycle synchrony among different species (protecting the newcomers in a recently reached area, previously colonized by other cicadas) seems to have played a significant role in the current system, so complex at first sight. The cycle shifts are so widespread that the most reasonable assumption is that, whichever the mechanism that triggers this accurate choreography consists of; whichever its biochemical or developmental details are; it was originated before the birth of the genus Magicicada itself, about 4 million years ago. Actually, this unique trait itself may have been the creative force in the evolution of these insects, the ultimate responsible of their diversification and success. This is, no doubt, a significant advance in our understanding of the Magicicada cycles, but how they were originated first and how they actually take place are still questions to be answered.