Social networks and the Spanish 15-M movement

A complex myriad of factors, many of them related with the global economic crisis, have given rise to a large number of social movements in the latest years. From the Occupy movement to the Arab Spring, or the more recent Turkish protests, most of these phenomena share a notorious fact: having the social networking and the Web 2.0 as key stones in their birth, organization and evolution.

Because of this, there is an increasing interest in understand the mechanisms responsible for the emergence of these social movements characterized by a massive use of new technologies and social media. A well-grounded scientific knowledge of such mechanisms would help us to understand the origins and ultimate motivations of the movements, their characteristic duration, impact and dynamics, and would also help to discern, for instance, between spontaneous popular movements and more centralized initiatives driven by private or governmental institutions.

Fortunately, the extensive use of new technologies, and in particular of social networks, provides an excellent tool for researchers to efficiently study the characteristics and features of these movements. The research work done by Borge-Holthoefer et al., from the University of Zaragoza (Spain) and the Institute for Scientific Interchange in Torino (Italy), constitutes a good example of this. In their recent work¹, Borge-Holthoefer and colleagues study, from the point of view of information networks, the emergence and evolution of the Spanish 15-M movement, a set of protests which started around May 15th of 2011 in several cities in Spain and then spread across the country. The movement attracted both national and international attention from the mass media, and constitutes an appealing example of a nation-level protest majorly coordinated by social networks.

In order to perform such a study, Borge-Holthoefer and colleagues analyzed a large set of short messages (tweets) from the social network Twitter. Using up to 70 labels or hashtags (such as #acampadasol or #nolesvotes) to identify the tweets related to the 15-M movement from a large Twitter database, they gathered more than 500,000 tweets from a total of approximately 85,000 users. The tweets corresponded to a full month of activity (from April 25th to May 26th), which included the formation and consolidation of the movement. A total of 3 million of followers where considered, which corresponds grossly with the audience estimated by Twitter in Spain.

The researchers studied this huge amount of information by building “information networks”: the users were considered as the nodes of the network, and if a user B received a tweet from user A, then a connection is established from node A to node B. This means that the connections are asymmetrical (the fact that B receives tweets from A does not necessarily mean that A receives tweets from B) and each connection has a particular strength (the larger the more tweets are received by B from A). In addition, it is worth noticing that the network structure evolves in time, as new users were continuously joining the network and sending new tweets.

Borge-Holthoefer and colleagues found that the emergent information network had indeed a high level of complexity. In particular, the network were found to be scale-free, which implies that a wide set of different scales in the transmission of information were observed. Looking at the number of tweets sent by each user, for instance, the network contains a large number of users who sent just a few tweets, and a smaller but still significant number of users who sent a large number of tweets (on the order of a thousand tweets); these users were identified as hubs, or massively-connected nodes, of the network. The probability P to find a user in the network who sent N tweets is given by a power-law distribution P =C· N^g, with C being a constant and the exponent taking a value of g =-2.3. Interestingly, the same distribution was also found when looking at the number of tweets received by each user, although the exponent of the power-law distribution was of g =-1.1 in this case.

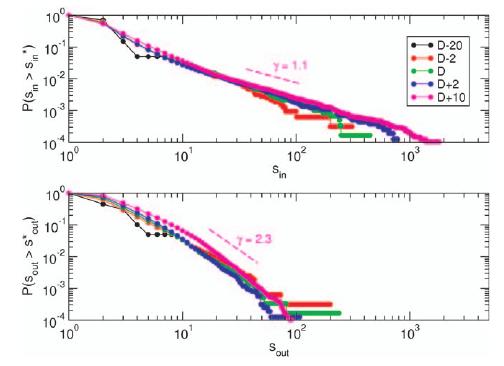
Among the pool of dynamical mechanisms which are known to produce scale-free networks, a prominent example is the Barabási-Albert algorithm ². This algorithm establishes that if new nodes are successively added to an initially small network, and they have preference to attach to previously existing nodes with high number of established connections, the resulting network will be scale-free with an exponent of g=-2. It is interesting to note that this value is close to the one found for the network of tweets sent by the users, and the authors propose indeed a variant of the Barabási-Albert algorithm (based on rank preferential attachment) to explain some additional features found in the network (such as the network “effervescence” or periods of intense activity and growth).

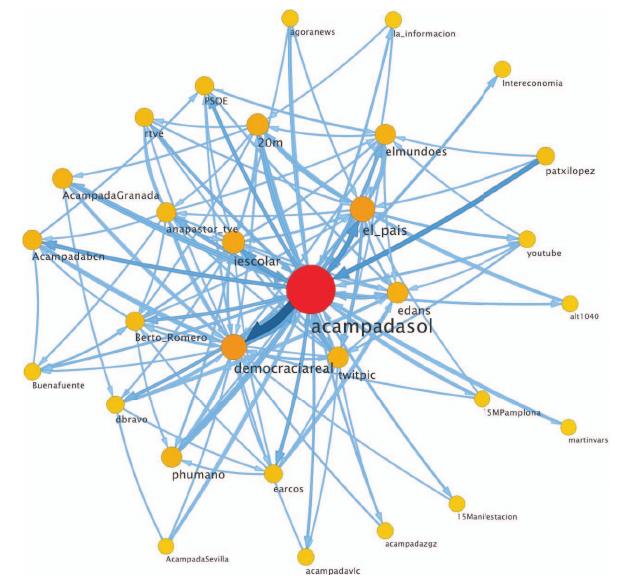
The study sheds light into several aspects of technical and social importance as well. For instance, when considering the network of tweets received, one can easily identify the hubs (or massively connected nodes) of the network as governmental institutions or mass media. On the other hand, these nodes tend to be poorly connected when one looks at the network of tweets sent. In other words, these nodes rarely re-tweet, and therefore they constitute information sinks that do not contribute to maintain the information flow and the “social temperature” of the network. It is ironic, indeed, that what a priori seems to be a good choice (targeting the government and the mass media) turns out to be harmful for information spreading in the whole network.

The existence of scale-free networks and other power-law distributions in nature is quite common, and it is usually linked to the existence of critical and/or self-organized behavior, in which the global phenomenon emerges as a consequence of the cooperation between a large number of interacting elements, instead of being driven by a single global driving force. Still, the emergence of global social movements constitutes an enormously complex phenomenon, and solid conclusions are hard to obtain. The study of social complex networks like the one performed in [ref. 1] constitutes only a first step in the process, and the analytical and numerical tools available for such studies are rapidly growing. With the help of interrelated disciplines such as complex networks theory, statistical mechanics and big data science, we might be soon closer to understand the origin of such an exciting cooperative emergent human behavior.